20 bài tập cơ bản Từ vuông góc đến song songLàm bàiCâu hỏi 1 : Em hãy chọn phát biểu sai trong các phát biểu sau:
Đáp án: C Phương pháp giải: Áp dụng tiên đề Ơ-clit về đường thẳng song song, dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết: - Hai đường thẳng không có điểm chung thì song song (đúng, theo định nghĩa hai đường thẳng song song) - Qua điểm M nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng ấy (đúng, theo tiên đề Ơ-clit) - Hai đường thẳng không cắt nhau là hai đường thẳng phân biệt. (sai, vì nó có thể là 2 đường thẳng trùng nhau) - Nếu một đường thẳng cắt hai đường thẳng tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song (đúng, theo dấu hiệu nhận biết hai đường thẳng song song) Chọn C. Câu hỏi 2 : Qua điểm M ở ngoài đường thẳng a cho trước, vẽ được bao nhiêu đường thẳng song song với đường thẳng đó?
Đáp án: A Phương pháp giải: Áp dụng tiên đề Ơ-clit. Lời giải chi tiết: Theo tiên đề Ơ-clit ta có: Qua điểm M ở ngoài đường thẳng a cho trước, vẽ được duy nhất một đường thẳng song song với đường thẳng đó. Chọn A. Câu hỏi 3 : Cho ba đường thẳng phân biệt \(a,\,b\) và \(c,\) biết \(a//c\) và \(b//c\). Kết luận nào đúng:
Đáp án: A Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. Lời giải chi tiết: Ta có: \(\left\{ \begin{align} & a//c \\ & b//c \\\end{align} \right.\Rightarrow a//\,b\) (hai đường thẳng cùng cùng song song với một đường thẳng thứ ba thì song song với nhau) Chọn A. Câu hỏi 4 : Cho ba đường thẳng phân biệt \(a,\,b\) và c, biết \(a//b\) và \(a\bot c\). Kết luận nào đúng:
Đáp án: B Phương pháp giải: Áp dụng tính chất: Hai đường thẳng song song, nếu đường thẳng thứ ba vuông góc với một trong hai đường thẳng đó thì nó vuông góc với đường thẳng còn lại. Lời giải chi tiết: Ta có: \(\left\{ \begin{align} & a//b \\ & a\,\bot c \\\end{align} \right.\Rightarrow \,b\bot c\) (quan hệ giữa tính vuông góc với tính song song) Chọn B Câu hỏi 5 : Trong các khẳng định sau, khẳng định nào sai?
Đáp án: B Phương pháp giải: Vận dụng kiến thức lý thuyết về quan hệ giữa tính vuông góc và tính song song của 3 đường thẳng để chọn đáp án phù hợp. Lời giải chi tiết: B sai. Vì trong quan hệ giữa tính vuông góc và tính song song của 3 đường thẳng: Nếu hai đường thẳng (phân biệt) cùng vuông góc với đường thẳng thứ ba thì song song với nhau. Câu hỏi 6 : Viết chữ cái đứng trước kèm điền (Đ) với câu trả lời đúng và (S) với câu trả lời sai dưới đây: Đường thẳng a song song với đường thẳng b. Đường thẳng c cắt đường thẳng b tạo một góc \({90^0}\) . Vậy:
Đáp án: D Phương pháp giải: Vẽ hình minh họa rồi chọn đáp án đúng. Lời giải chi tiết:
Từ giả thiết đề bài cho ta có: \(\left\{ \begin{array}{l}a//b\,\\c \bot b\end{array} \right. \Rightarrow c \bot a\) Vậy đường thẳng c vuông góc với đường thẳng a. Chọn D Câu hỏi 7 : Cho \(a,b,c\) là ba đường thẳng phân biệt. Biết \(a \bot b\) và \(b \bot c\) thì kết luận nào sau đây đúng?
Đáp án: A Phương pháp giải: Quan sát hình vẽ: Trong mặt phẳng Oxy, nếu \(a \bot b\) và \(b \bot c\) thì \(c//a\)
Lời giải chi tiết:
Quan sát hình vẽ: Trong mặt phẳng Oxy, nếu \(a \bot b\) và \(b \bot c\) thì \(c//a\) Chọn A. Câu hỏi 8 : Cho ba đường thẳng phân biệt \(a,\,b\) và c, biết \(a//b\) và \(a \bot c\). Kết luận nào đúng:
Đáp án: B Phương pháp giải: Áp dụng tính chất: Hai đường thẳng song song, nếu đường thẳng thứ ba vuông góc với một trong hai đường thẳng đó thì nó vuông góc với đường thẳng còn lại. Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}a//b\\a\, \bot c\end{array} \right. \Rightarrow \,b \bot c\)(quan hệ giữa tính vuông góc với tính song song) Chọn B. Câu hỏi 9 : Cho ba đường thẳng phân biệt a, b, c, biết \(a//b\) và \(b//c\) . Chọn kết luận đúng:
Đáp án: A Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}a//c\\b//c\end{array} \right. \Rightarrow a//\,b\)(hai đường thẳng cùng cùng song song với một đường thẳng thứ ba thì song song với nhau) Chọn A. Câu hỏi 10 : Chứng minh định lý là
Đáp án: A Phương pháp giải: Sử dụng định nghĩa “chứng minh định lý”. Lời giải chi tiết: Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận. Chọn A. Câu hỏi 11 : Trong các câu sau, câu nào cho một định lí
Đáp án: A Phương pháp giải: Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí. Lời giải chi tiết: Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.” Chọn A. Câu hỏi 12 : Chọn câu đúng.
Đáp án: D Phương pháp giải: Sử dụng lý thuyết về định lý. Lời giải chi tiết: Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Chọn D. Câu hỏi 13 : Em hãy chọn phát biểu sai trong các phát biểu sau:
Đáp án: C Phương pháp giải: Áp dụng tiên đề Ơ-clit về đường thẳng song song, dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết: - Hai đường thẳng không có điểm chung thì song song (đúng, theo định nghĩa hai đường thẳng song song) - Qua điểm M nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng ấy (đúng, theo tiên đề Ơ-clit) - Hai đường thẳng không cắt nhau là hai đường thẳng phân biệt. (sai, vì nó có thể là 2 đường thẳng trùng nhau) - Nếu một đường thẳng cắt hai đường thẳng tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song (đúng, theo dấu hiệu nhận biết hai đường thẳng song song) Chọn C. Câu hỏi 14 : Qua điểm M ở ngoài đường thẳng a cho trước, vẽ được bao nhiêu đường thẳng song song với đường thẳng đó?
Đáp án: A Phương pháp giải: Áp dụng tiên đề Ơ-clit. Lời giải chi tiết: Theo tiên đề Ơ-clit ta có: Qua điểm M ở ngoài đường thẳng a cho trước, vẽ được duy nhất một đường thẳng song song với đường thẳng đó. Chọn A. Câu hỏi 15 : Qua điểm \(A\) ở ngoài đường thẳng \(xy\) cho trước ta vẽ được bao nhiêu đường thẳng song song với đường thẳng \(xy\) ?
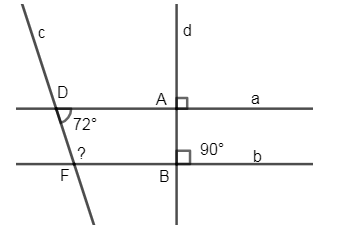
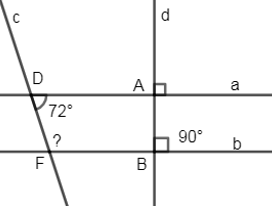
Đáp án: C Phương pháp giải: Nhớ lại tiên đề Ơ-cơ-lít: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó. Lời giải chi tiết: Theo tiên đề Ơ-cơ-lít: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó. Vậy nên: Qua điểm \(A\) ở ngoài đường thẳng \(xy\) cho trước ta vẽ được một và chỉ một đường thẳng song song với đường thẳng \(xy\). Chọn C Câu hỏi 16 : Cho hình vẽ sau:
Biết \(a\bot d,\,b\bot d,\,\widehat{A\text{D}F}={{72}^{0}}\). Tính \(\widehat{DFB}\).
Đáp án: D Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. - Tính chất hai đường thẳng song song. Lời giải chi tiết: Vì \(\left\{ \begin{align} & a\bot d \\ & b\bot d \\\end{align} \right.\Rightarrow a\,//\,b\) (quan hệ giữa tính vuông góc với tính song song)
\(\Rightarrow \widehat{ADF}+\widehat{DFB}={{180}^{0}}\Rightarrow \widehat{DFB}={{180}^{0}}-\widehat{ADF}={{180}^{0}}-{{72}^{0}}={{108}^{0}}\) (2 góc trong cùng phía bù nhau) Chọn D. Câu hỏi 17 : Cho hình vẽ sau:
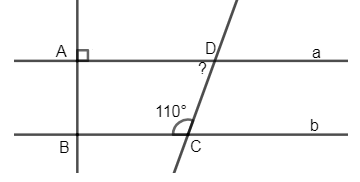
Biết \(a//\,b,\,\widehat{BC\text{D}}={{110}^{0}}\). Kết luận nào sau đây là đúng:
Đáp án: B Phương pháp giải: Áp dụng tính chất: Hai đường thẳng song song, nếu đường thẳng thứ ba vuông góc với một trong hai đường thẳng đó thì nó vuông góc với đường thẳng còn lại. - Tính chất hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\left\{ \begin{align} & a\,//\,b \\ & AB\bot a \\\end{align} \right.\Rightarrow AB\bot b\) (quan hệ giữa tính vuông góc với tính song song)
Vì \(a//\,b\left( gt \right)\Rightarrow \widehat{A\text{D}C}+\widehat{BC\text{D}}={{180}^{0}}\) (2 góc trong cùng phía bù nhau) \(\Rightarrow \widehat{A\text{D}C}={{180}^{0}}-\widehat{BC\text{D}}={{180}^{0}}-{{110}^{0}}={{70}^{0}}\) Chọn B Câu hỏi 18 : Cho hình vẽ sau: a) Vì sao \(a//\,b?\) b) Tính \(\widehat{BNM}\)
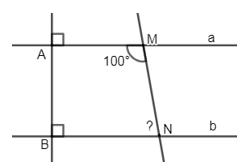
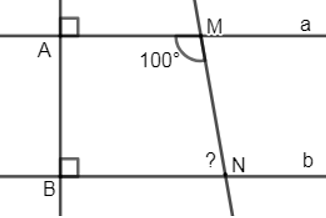
Đáp án: A Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. - Tính chất hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\left\{ \begin{align} & a\bot AB \\ & b\bot AB \\\end{align} \right.\left( gt \right)\Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song) \(\Rightarrow \widehat{AMN}+\widehat{BNM}={{180}^{0}}\Rightarrow \widehat{BNM}={{180}^{0}}-{{100}^{0}}={{80}^{0}}\) (2 góc trong cùng phía bù nhau) Chọn A Câu hỏi 19 : Cho hình vẽ sau: Biết \(c\bot a,\,\widehat{{{C}_{1}}}={{45}^{0}},\,\widehat{{{B}_{1}}}={{135}^{0}}\) . Chứng minh \(b\bot c\) . Phương pháp giải: Áp dụng tính chất: Hai đường thẳng song song, nếu đường thẳng thứ ba vuông góc với một trong hai đường thẳng đó thì nó vuông góc với đường thẳng còn lại. - Áp dụng dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\widehat{{{B}_{1}}}+\widehat{{{B}_{2}}}={{180}^{0}}\) (kề bù) \(\begin{align} & \Rightarrow \widehat{{{B}_{2}}}={{180}^{0}}-\widehat{{{B}_{1}}}={{180}^{0}}-{{135}^{0}}={{45}^{0}} \\ & \Rightarrow \widehat{{{B}_{2}}}=\widehat{{{C}_{1}}}\left( ={{45}^{0}} \right) \\\end{align}\) Mà \(\widehat{{{B}_{2}}}\) và \(\widehat{{{C}_{1}}}\) là hai góc đồng vị nên suy ra \(a//\,b\)(dấu hiệu nhận biết hai đường thẳng song song) Lại có, \(c\bot a\left( gt \right)\Rightarrow b\bot c\) (quan hệ giữa tính vuông góc với tính song song) Câu hỏi 20 : Ở hình vẽ dưới đây, ta có \(\angle {A_1}\) và \(\angle {B_1}\) là cặp góc
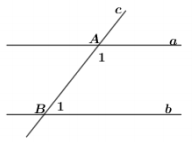
Đáp án: A Phương pháp giải: Căn cứ vào vị trí của góc so với hai đường thẳng và đường thẳng thứ ba mà ta xác định được vị trí của hai góc \(\angle {A_1}\) và \(\angle {B_1}\). Lời giải chi tiết: Trong hình vẽ bên ta thấy \(\angle {A_1}\) và \(\angle {B_1}\) là hai cặp góc trong cùng phía. Chọn A
|