20 bài tập trắc nghiệm hàm số lượng giác mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \cos 2x + \cos x\). Khi đó \(M + m\) bằng bao nhiêu?
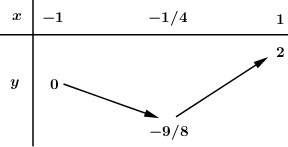
Đáp án: D Phương pháp giải: Đặt \(\cos \,x = t,\,\,\,t \in \left[ { - 1;1} \right]\). Tìm GTLN, GTNN của hàm số \(y = f\left( t \right) = 2{t^2} + t - 1\) trên đoạn \(\left[ { - 1;1} \right]\) bằng cách lập BBT. Lời giải chi tiết: Ta có: \(y = \cos 2x + \cos x = 2{\cos ^2}x + \cos x - 1\). Đặt \(\cos {\mkern 1mu} x = t,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} t \in \left[ { - 1;1} \right]\). Hàm số trở thành \(y = 2{t^2} + t - 1\). Đây là 1 parabol có bề lõm hướng lên, có hoành độ đỉnh \(x = - \dfrac{b}{{2a}} = - \dfrac{1}{4}\). BBT: Dựa vào BBT ta có: \(M = 2,\,\,m = - \dfrac{9}{8}\), Vậy \(M + m = 2 - \dfrac{9}{8} = \dfrac{7}{8}\). Chọn D.
Câu hỏi 2 : Có bao nhiêu giá trị \(x \in \left[ {0;5\pi } \right]\) để hàm số \(y = \tan x\) nhận giá trị bằng 0?
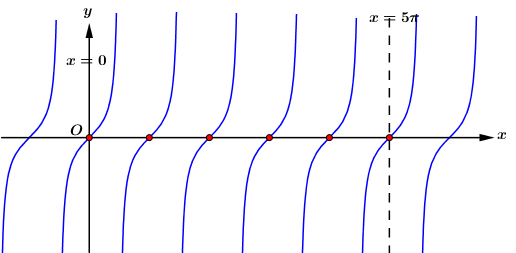
Đáp án: D Phương pháp giải: Vẽ đồ thị hàm số \(y = \tan x\) trên đoạn \(\left[ {0;5\pi } \right]\), xác định số giao điểm của đồ thị hàm số với trục hoành. Lời giải chi tiết: Ta vẽ đồ thị hàm số \(y = \tan x\) trên đoạn \(\left[ {0;5\pi } \right]\).
Dựa vào đồ thị hàm số ta thấy trên đoạn \(\left[ {0;5\pi } \right]\), đồ thị hàm số cắt trục hoành tại 6 điểm phân biệt (điểm màu đỏ), do đó có 6 giá trị \(x \in \left[ {0;5\pi } \right]\) để hàm số \(y = \tan x\) nhận giá trị bằng 0. Chọn D. Câu hỏi 3 : Khẳng định nào sau đây là đúng?
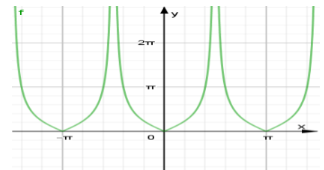
Đáp án: B Phương pháp giải: - Từ đồ thị hàm số \(y = \tan x\) vẽ đồ thị hàm số \(y = \left| {\tan x} \right|\) bằng cách giữa lại phần đồ thị nằm phía trên trục Ox, lấy đối xứng phần đồ thị phía dưới trục Ox qua trục Ox sau đó xóa đi phần đồ thị phía dưới trục Ox. - Dựa vào đồ thị hàm số \(y = \left| {\tan x} \right|\) vẽ được để chọn đáp án đúng. Lời giải chi tiết: Ta có đồ thị hàm số \(y = \left| {\tan x} \right|\) như sau:
TXĐ: \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\). Dựa vào đồ thị hàm số ta thấy: - Hàm số \(y = \left| {\tan x} \right|\) nghịch biến trên \(\left( { - \dfrac{\pi }{2};0} \right)\) và đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\), do đó đáp án A và D sai. - Đặt \(f\left( x \right) = \left| {\tan x} \right|\), \(\forall x \in D \Rightarrow - x \in D\). \(f\left( { - x} \right) = \left| {\tan \left( { - x} \right)} \right| = \left| { - \tan x} \right| = \left| {\tan x} \right| = f\left( x \right)\), do đó hàm số đã cho là hàm chẵn trên tập xác định. Do đó đáp án B đúng. - Do là hàm chẵn nên đồ thị hàm số đối xứng qua trục Oy chứ không đố Chọn B. Câu hỏi 4 : Xét sự biến thiên của hàm số \(y = \sin x - \cos x\). Trong các kết luận sau, kết luận nào đúng?
Đáp án: A Phương pháp giải: - Biến đổi: \(\sin x - \cos x = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\). - Xác định chu kì tuần hoàn của hàm số và suy ra các khoảng đơn điệu của hàm số. - Hàm số \(y = \sin x\) đồng (nghịch) biến trên \(\left( {a;b} \right)\) thì hàm số \(y = \sin \left( {x - k} \right)\) đồng (nghịch) biến trên khoảng \(\left( {a + k;b + k} \right)\). Lời giải chi tiết: - \sqrt 2 ;\sqrt 2 } \right]\), do đó loại đáp án C. Hàm số đã cho tuần hoàn với chu kì \(2\pi \), ta xét sự biến thiên của hàm số trên đoạn \(\left[ { - \dfrac{\pi }{4};\dfrac{{7\pi }}{4}} \right]\). - Hàm số \(y = \sin x\) đồng biến trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) nên hàm số \(y = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\) nghịch biến trên \(\left( { - \dfrac{\pi }{4};\dfrac{{3\pi }}{4}} \right)\). - Hàm số \(y = \sin x\) đồng biến trên \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\) nên hàm số \(y = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\) nghịch biến trên \(\left( {\dfrac{{3\pi }}{4};\dfrac{{7\pi }}{4}} \right)\). Chọn A. Câu hỏi 5 : Tìm tập giá trị của hàm số \(y = \sqrt 3 \sin 2x - \cos 2x + 2019.\)
Đáp án: C Phương pháp giải: Sử dụng các công thức lượng giác, biến đổi và tìm tập giá trị của hàm số. Lời giải chi tiết: Ta có: \(y = \sqrt 3 \sin 2x - \cos 2x + 2019\) \(\begin{array}{l} \Rightarrow y = 2\left( {\frac{{\sqrt 3 }}{2}\sin 2x - \frac{1}{2}\cos 2x} \right) + 2019\\\,\,\,\,\,\,\,\,\,\,\,\, = 2\left( {\sin 2x.\cos \frac{\pi }{6} - \cos 2x.\sin \frac{\pi }{6}} \right) + 2019\\\,\,\,\,\,\,\,\,\,\,\,\, = 2\sin \left( {2x - \frac{\pi }{6}} \right) + 2019.\end{array}\) Ta có: \( - 1 \le \sin \left( {2x + \frac{\pi }{6}} \right) \le 1 \Rightarrow - 2 \le 2\sin \left( {2x + \frac{\pi }{6}} \right) \le 2\) \(\begin{array}{l} \Rightarrow - 2 + 2019 \le 2\sin \left( {2x + \frac{\pi }{6}} \right) + 2019 \le 2 + 2019\\ \Rightarrow 2017 \le 2\sin \left( {2x + \frac{\pi }{6}} \right) + 2019 \le 2021.\\ \Rightarrow G = \left[ {2017;\,\,2021} \right].\end{array}\) Chọn C. Câu hỏi 6 : Trong các hàm số dưới đây có bao nhiêu hàm số là hàm số chẵn: \(y = \cos 3x\), \(y = \sin \left( {{x^2} + 1} \right)\), \(y = {\tan ^2}x\), \(y = \cot x\)
Đáp án: D Phương pháp giải: Hàm số \(y = f\left( x \right)\) có TXĐ là D được gọi là hàm số chẵn nếu \(\forall x \in D \Rightarrow - x \in D\) và \(f\left( x \right) = f\left( { - x} \right)\). Lời giải chi tiết: - Xét hàm số \(y = f\left( x \right) = \cos 3x\). TXĐ: \(D = \mathbb{R} \Rightarrow x \in D\) thì \( - x \in D\). Ta có: \(f\left( { - x} \right) = \cos \left( { - 3x} \right) = \cos 3x = f\left( x \right)\). Do đó hàm số \(y = f\left( x \right) = \cos 3x\) là hàm số chẵn. - Xét hàm số \(y = f\left( x \right) = \sin \left( {{x^2} + 1} \right)\) TXĐ: \(D = \mathbb{R} \Rightarrow x \in D\) thì \( - x \in D\). Ta có: \(f\left( { - x} \right) = \sin \left[ {{{\left( { - x} \right)}^2} + 1} \right] = \sin \left( {{x^2} + 1} \right) = f\left( x \right)\). Do đó hàm số \(y = f\left( x \right) = \sin \left( {{x^2} + 1} \right)\) là hàm số chẵn. - Xét hàm số \(y = f\left( x \right) = {\tan ^2}x\) TXĐ: \(D = \mathbb{R} \Rightarrow x \in D\) thì \( - x \in D\). Ta có: \(f\left( { - x} \right) = {\left[ {\tan \left( { - x} \right)} \right]^2} = {\left( { - \tan x} \right)^2} = {\tan ^2}x = f\left( x \right)\). Do đó hàm số \(y = f\left( x \right) = {\tan ^2}x\) là hàm số chẵn. - Xét hàm số \(y = f\left( x \right) = \cot x\) TXĐ: \(D = \mathbb{R} \Rightarrow x \in D\) thì \( - x \in D\). Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) = - \cot x = - f\left( x \right)\). Do đó hàm số \(y = f\left( x \right) = \cot x\) là hàm số lẻ. Vậy trong các hàm số đã cho có 3 hàm số là hàm số chẵn. Chọn D. Câu hỏi 7 : Tìm giá trị lớn nhât, giá trị nhỏ nhất của hàm số: \(y = 3 + \sqrt {4 - 3{{\sin }^2}x} \)
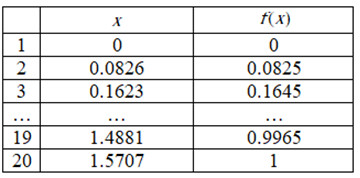
Đáp án: D Phương pháp giải: Lời giải chi tiết: \(y = 3 + \sqrt {4 - 3{{\sin }^2}x} \) Nhập: \(\left\{ \begin{array}{l}F\left( x \right) = 3 + \sqrt {4 - 3{{\sin }^2}x} \\Start:0\\End:2\pi \\Step:\frac{{End - Start}}{{19}} = \frac{{2\pi }}{{19}}\end{array} \right.\) Nhìn cột \(F\left( x \right)\)nhận thấy: \(\left\{ \begin{array}{l}Max\,f\left( x \right) = 5\\Min\,f\left( x \right) \approx 4\left( { = 4,0101} \right)\end{array} \right.\) Chọn D. Câu hỏi 8 : Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \sqrt 2 {\cos ^2}\left( {x + \frac{\pi }{4}} \right) + 1\) theo thứ tự là:
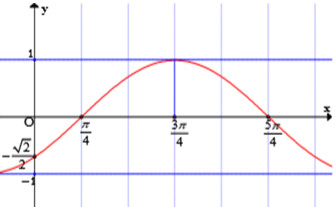
Đáp án: A Phương pháp giải: Lời giải chi tiết: \(y = \sqrt 2 {\cos ^2}\left( {x + \frac{\pi }{4}} \right) + 1\) Nhập: \(\left\{ \begin{array}{l}F\left( x \right) = \sqrt 2 {\cos ^2}\left( {x + \frac{\pi }{4}} \right) + 1\\Start = 0\\End = 2\pi \\Step = \frac{{End - Start}}{{19}} = \frac{{2\pi }}{{19}}\end{array} \right.\) Nhìn cột \(F\left( x \right)\)thấy: \(\left\{ \begin{array}{l}Min\,f\left( x \right) \approx 1\left( { = 1,0216} \right)\\Max\,f\left( x \right) \approx 1 + \sqrt 2 \left( { = 2,4117} \right)\end{array} \right.\) Chọn A. Câu hỏi 9 : Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
Hàm số đó là hàm số nào?
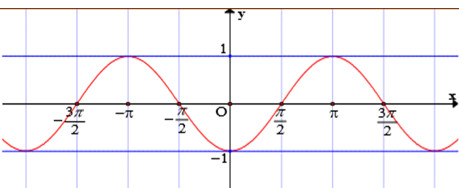
Đáp án: B Phương pháp giải: Lời giải chi tiết: Dựa vào đồ thị, thấy đường cong đi qua các điểm: \(\begin{array}{l}x = 0,y = - \dfrac{{\sqrt 2 }}{2}\\x = \dfrac{\pi }{4},y = 0\\x = \dfrac{{3\pi }}{4},y = 1\\x = \dfrac{{5\pi }}{4},y = 0\end{array}\) \( \to \) Thế vào các đáp án A, B, C, D: Thấy B thoả mãn. Chọn B. Câu hỏi 10 : Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án \(A,B,C,D\). Hỏi hàm số đó là hàm số nào?
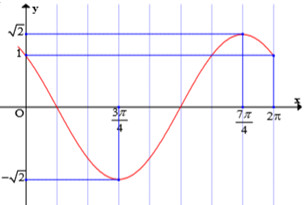
Đáp án: A Phương pháp giải: Lời giải chi tiết: Dựa vào đồ thị, thấy đường cong đi qua các điểm \(\begin{array}{l}x = 0,y = 1\\x = \dfrac{{3\pi }}{4},y = - \sqrt 2 \\x = \dfrac{{7\pi }}{4},y = \sqrt 2 \\x = 2\pi ,y = 1\end{array}\) \( \to \) Thế vào các đáp án A, B, C, D: Thấy A thoả mãn. Chọn A. Câu hỏi 11 : Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
Đáp án: C Phương pháp giải: Lời giải chi tiết: Dựa vào đồ thị, thấy đường cong đi qua các điểm: \(\begin{array}{l}x = \dfrac{{ - 3\pi }}{2},y = 0\\x = - \pi ,y = 1\\x = - \dfrac{\pi }{2},y = 0\\x = 0,y = - 1\end{array}\) Thế vào các đáp án \( \to \) Chỉ thấy C thoả mãn. Chọn C. Câu hỏi 12 : Hàm số sau hàm số nào đồng biến trên khoảng \(\left( { - \frac{\pi }{2};0} \right)\) và nghịch biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)
Đáp án: D Phương pháp giải: Lời giải chi tiết: Xét đáp án A: \(y = {\sin ^2}x.\) Dùng MODE + 7 (máy tính cầm tay) Nhập: \(\left\{ \begin{array}{l}f(x) = {\sin ^2}x\\Start = - \frac{\pi }{2}\\End = 0\\Step = \frac{{End - Start}}{{19}} = \frac{\pi }{2}:19\end{array} \right.\) Nhìn bảng, thấy: \(x\) tăng thì \(f\left( x \right)\) giảm \( \Rightarrow \) Hàm số nghịch biến trong \(\left( { - \frac{\pi }{2};0} \right)\) \( \Rightarrow \) Loại. Xét đáp án B: \(y = 6 - \sin x.\) Dùng MODE +7 (máy tính cầm tay) Nhập \(\left\{ \begin{array}{l}f(x) = 6 - \sin x\\Start = - \frac{\pi }{2}\\End = 0\\Step = \frac{{End - Start}}{{19}} = \frac{\pi }{2}:19\end{array} \right.\) Nhìn bảng, thấy: \(x\) tăng thì \(f\left( x \right)\) giảm \( \Rightarrow \) Hàm số nghịch biến trên \(\left( { - \frac{\pi }{2};0} \right)\) \( \Rightarrow \) Loại. Xét đáp án C: \(y = 3 - 2\sin x.\) Dùng MODE + 7 (máy tính cầm tay) Nhập \(\left\{ \begin{array}{l}f(x) = 3 - 2\sin x\\Start = - \frac{\pi }{2}\\End = 0\\Step = \frac{{End - Start}}{{19}} = \frac{\pi }{2}:19\end{array} \right.\) Nhìn bảng, thấy: \(x\) tăng thì \(f\left( x \right)\) giảm \( \Rightarrow \) Hàm số nghịch biến trên \(\left( { - \frac{\pi }{2};0} \right)\) \( \Rightarrow \) Loại. Xét đáp án D: \(y = 2 - 2{\sin ^2}x.\) Dùng MODE + 7 (máy tính cầm tay). Nhập: \(\left\{ \begin{array}{l}f\left( x \right) = 2 - 2{\sin ^2}x\\Start = - \frac{\pi }{2}\\End = 0\\Step = \frac{{End - Start}}{{19}} = \frac{\pi }{2}:19\end{array} \right.\) Nhìn bảng, thấy: \(x\) tăng thì \(f\left( x \right)\) tăng \( \Rightarrow \) Hàm số đồng biến trên \(\left( { - \frac{\pi }{2};0} \right)\) Nhập: \(\left\{ \begin{array}{l}f\left( x \right) = 2 - 2{\sin ^2}x\\Start = 0\\End = \frac{\pi }{2}\\Step = \frac{{End - Start}}{{19}} = \frac{\pi }{2}:19\end{array} \right.\) \( \Rightarrow \) Hàm số nghịch biến trên \(\left( {0;\frac{\pi }{2}} \right)\) Chọn D. Câu hỏi 13 : Giá trị nhỏ nhất của hàm số \(y = \dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}}\) là:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Sử dụng máy tính: MODE 7: Nhập hàm số Start: 0, End: \(2\pi \), Step: \(2\pi :19\) \( \Rightarrow \) Quan sát giá trị cột \(f(x)\), ta thấy: \(\min y = 0.1821 \approx \dfrac{2}{{11}}.\) Chọn A. Câu hỏi 14 : Trong khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\), hai hàm số nào sau đây cùng đồng biến?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Kiểm tra tính đơn điệu của các hàm số: \(y = \sin x,y = \cos x,y = \cot x,y = \tan x\). Sử dụng máy tính MODE 7: Start: 0 End: \(\dfrac{\pi }{2}\) Step: \(\dfrac{\pi }{2}:19\) \( \to \) Nhận thấy các giá trị cột \(f\left( x \right)\) luôn tăng. \( \to \) Hàm số \(y = \sin x\) luôn đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\). Làm tương tự với các hàm số Thấy có thêm hàm số là hàm đồng biến. Chọn B.
Câu hỏi 15 : Với \(x \in \left( {0;\dfrac{\pi }{2}} \right)\), mệnh đề nào sau đây sai?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Kiểm tra tính đơn điệu của các hàm số \(y = \sin x,\,\,y = \cos x,\,\,y = \cot x,\,\,y = \tan x\) Sử dụng máy tính MODE 7: + Thử đáp án D: Nhập hàm số: \(y = \cos x.\) \(Start:{\rm{ }}0,\,\,End:\dfrac{\pi }{2},\,\,Step:\dfrac{\pi }{2}:19\) \( \to \) Quan sát giá trị cột \(f\left( x \right)\) thấy giá trị luôn tăng. Chọn D. Câu hỏi 16 : Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
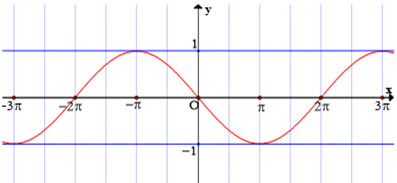
Đáp án: A Phương pháp giải: Lời giải chi tiết: Dựa vào đồ thị, thấy đường cong đi qua các điểm \(\left( {0;0} \right),\,\,\left( { - \pi ; - 1} \right),\,\,\left( { - 3\pi ; - 1} \right)\). \( \to \) Thay \(\left[ \begin{array}{l}x = 0\\x = - \pi \\x = - 3\pi \end{array} \right.\) vào 4 đáp án \( \Rightarrow \) Chỉ đáp án A thoả mãn \(\left\{ \begin{array}{l}x = 0,y = 0\\x = - \pi ,y = 1\\x = - 3\pi ,y = - 1\end{array} \right..\) Chọn A. Câu hỏi 17 : Trên đoạn \(\left[ {0;2\pi } \right]\) hàm số \(y = \sin x\) đồng biến trên những khoảng nào?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Kiểm tra tính đơn điệu của hàm số \(y = \sin x\) bằng MODE 7 Thử từng đáp án: Đáp án A: \(\begin{array}{l}Start:0\\End:\pi \\Step:\dfrac{\pi }{{19}}\end{array}\)\( \to \)Quan sát thấy giá trị cột \(f(x)\) vừa tăng vừa giảm \( \to \) Sai. Làm tương tự, chỉ thấy trên \(\left( {0;\dfrac{\pi }{2}} \right)\) và \(\left( {\dfrac{{3\pi }}{2};2\pi } \right)\) hàm số chỉ luôn tăng. Chọn D. Câu hỏi 18 : Hàm số \(y = \dfrac{{2 - \sin 2x}}{{\sqrt {m\cos x + 1} }}\) có tập xác định là \(\mathbb{R}\) khi:
Đáp án: D Phương pháp giải: - Hàm số \(y = \dfrac{1}{{\sqrt A }}\) xác định khi và chỉ khi \(A > 0\). - Chia các trường hợp \(m = 0,\,\,m > 0,\,\,m < 0\) và đánh giá. Lời giải chi tiết: Hàm số có tập xác định là R khi và chỉ khi \(m\cos x + 1 > 0\,\,\forall x \in \mathbb{R}\). Khi m = 0 thì ta có 1 > 0 (luôn đúng). Khi m > 0 ta có: \( - 1 \le \cos x \le 1\,\,\forall x \in \mathbb{R}\) \( \Rightarrow - m \le m\cos x \le m\,\,\forall x \in \mathbb{R}\) \( \Leftrightarrow 1 - m \le m\cos x + 1 \le 1 + m\,\,\forall x \in \mathbb{R}\). Do đó \(m\cos x + 1 > 0\,\,\forall x \in \mathbb{R}\) khi và chỉ khi \(1 - m > 0 \Leftrightarrow m < 1\). Kết hợp điều kiện \( \Rightarrow 0 < m < 1\). Khi m < 0 ta có: \( - 1 \le \cos x \le 1\,\,\forall x \in \mathbb{R}\) \( \Rightarrow - m \ge m\cos x \ge m\,\,\forall x \in \mathbb{R}\) \( \Leftrightarrow 1 - m \ge m\cos x + 1 \ge 1 + m\,\,\forall x \in \mathbb{R}\). Do đó \(m\cos x + 1 > 0\,\,\forall x \in \mathbb{R}\) khi và chỉ khi \(1 + m > 0 \Leftrightarrow m > - 1\). Kết hợp điều kiện \( \Rightarrow - 1 < m < 0\). Vậy \( - 1 < m < 1\). Chọn D. Câu hỏi 19 : Hàm số nào sau đây không chẵn, không lẻ?
Đáp án: C Phương pháp giải: - Tìm TXĐ của các hàm số. - Chọn \(x \in D\) sao cho \( - x \in D\) và \(f\left( x \right) \ne f\left( { - x} \right)\). Lời giải chi tiết: Xét hàm số \(y = f\left( x \right) = \sin 2x + \cos 2x\) có TXĐ \(D = \mathbb{R}\). Chọn \(x = \dfrac{\pi }{8} \in D\) \( \Rightarrow - x = - \dfrac{\pi }{8} \in D\). Ta có: \(f\left( {\dfrac{\pi }{8}} \right) = 3\sqrt 2 ,\,\,f\left( { - \dfrac{\pi }{8}} \right) = 2\sqrt 2 \). Vì \(f\left( {\dfrac{\pi }{8}} \right) \ne f\left( { - \dfrac{\pi }{8}} \right)\) nên hàm số \(y = f\left( x \right) = \sin 2x + \cos 2x\) là hàm không chẵn không lẻ. Chọn C. Câu hỏi 20 : Hàm số y = \(\frac{{\cos x + \sin x}}{{3 + m.\cos x}}\) xác định với mọi x R khi nào ?
Đáp án: C Phương pháp giải: Xét mẫu của hàm số :\(3 + m\cos x \ne 0;\forall x \in \mathbb{R}\). Lời giải chi tiết: Hàm số \(y = \frac{{\cos x + \sin x}}{{3 + m.\cos x}}\) xác định với mọi \(x \in \mathbb{R}\)\( \Leftrightarrow 3 + m\cos x \ne 0;\forall x \in \mathbb{R}\, \Leftrightarrow m\cos x \ne - 3\,\,\,\forall x \in \mathbb{R}\,\,\left( 1 \right)\) Ta có: \(\left| {\cos x} \right| \le 1 \Rightarrow \left| {m\cos x} \right| \le \left| m \right| \Leftrightarrow \left| {m\cos x} \right| \in \left[ {0;\,\left| m \right|} \right].\) Lại có: \(\left( 1 \right) \Leftrightarrow m\cos x \ne - 3\forall x \in \mathbb{R} \Leftrightarrow \left| {m\cos x} \right| \ne 3 \Rightarrow 3 \notin \left[ {0;\,\,\left| m \right|} \right]\) \( \Leftrightarrow \left[ \begin{array}{l}\left| m \right| < 3\\3 < 0\,\,\,\left( {kmt} \right)\end{array} \right. \Leftrightarrow \left| m \right| < 3.\) Chọn C.
|