20 bài tập cơ bản Ôn tập chương 2: Hàm số và đồ thịLàm bàiCâu hỏi 1 : Cho hàm số y = f (x) = \(\frac{1}{3}\)x2 - 1 thì:
Đáp án: C Phương pháp giải: Ta lần lượt tính các f để kiểm tra xem kết quả nào đúng. Lời giải chi tiết: \(f(0)=\frac{1}{3}{{.0}^{2}}-1=-1\), \(f(3)=\frac{1}{3}{{.3}^{2}}-1=2\) , \(f(-1)=\frac{1}{3}.{{(-1)}^{2}}-1=\frac{-2}{3}\) Chọn C. Câu hỏi 2 : Hàm số \(y=\frac{-2}{3}x\) nhận giá trị dương khi
Đáp án: A Phương pháp giải: Dựa vào quy tắc dấu để tìm điều kiện của x. Lời giải chi tiết: Do \(\frac{-2}{3}<0\) nên để \(y=\frac{-2}{3}x\) nhận giá trị dương thì \(x<0\). Chọn A. Câu hỏi 3 : Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a (a\(\ne \)0) thì đại lượng x tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ là:
Đáp án: B Phương pháp giải: Áp dụng định nghĩa của hai đại lượng tỉ lệ nghịch Lời giải chi tiết: Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a (a\(\ne \)0) thì đại lượng x tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ là a Chọn B. Câu hỏi 4 : Điểm A(1; 2) trong mặt phẳng tọa độ Oxy thuộc góc phần tư thứ:
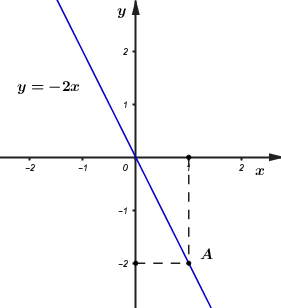
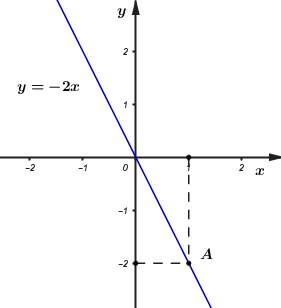
Đáp án: A Phương pháp giải: Dựa vào khái niệm mặt phẳng tọa độ. Lời giải chi tiết: Điểm A(1; 2) có hoành độ và tung độ dương nên nó thuộc góc phần tư thứ I. Chọn A . Câu hỏi 5 : Cho hàm số y = -2x. 1. Vẽ đồ thị của hàm số đã cho. 2. Điểm Q(-35; 70) có thuộc đồ thị của hàm số đã cho hay không? Vì sao?
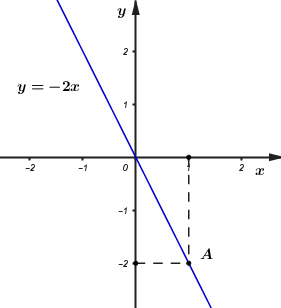
Đáp án: C Phương pháp giải: 1. Tìm một điểm bất kì có hoành độ khác 0 thuộc hàm số đã cho. Đồ thị của hàm số đã cho là đường thẳng đi qua gốc tọa độ và điểm thuộc hàm số đã cho đã tìm được. 2. Điểm \(M\left( {{x}_{0}};\ {{y}_{0}} \right)\) thuộc đồ thị của hàm số \(y=f\left( x \right)\) nếu \({{y}_{0}}=f\left( {{x}_{0}} \right).\) Lời giải chi tiết: 1. Vẽ đồ thị hàm số \(y=-2\text{x}\). - Khi x = 1 thì \(y=(-2).1=-2\). Vậy điểm A(1;\(-2\)) thuộc đồ thị của hàm số \(y=-2\text{x}\). Đồ thị của hàm số \(y=-2x\) là đường thẳng OA trong hình vẽ dưới. 2. Thay \(x=-35\) vào \(y=-2\text{x}\) ta được: \(y=(-2).(-35)=70\). Vậy \(Q\left( -35;\ 70 \right)\) thuộc đồ thị hàm số \(y=-2\text{x}\).
Câu hỏi 6 : Cho hàm số \(y = f\left( x \right) = - \frac{1}{4}{x^3}\) ta có \(f\left( { - 2} \right)\) bằng :
Đáp án: B Phương pháp giải: Thay \(x = - 2\) vào hàm số \(y = f\left( x \right) = - \frac{1}{4}{x^3}\). Lời giải chi tiết: Thay \(x = - 2\) vào hàm số \(y = f\left( x \right) = - \frac{1}{4}{x^3}\). Ta có: \(f\left( { - 2} \right) = - \frac{1}{4}{\left( { - 2} \right)^3} = - \frac{1}{4}.\left( { - 8} \right) = 2\) Vậy \(f\left( { - 2} \right) = 2\) Chọn B Câu hỏi 7 : Cho hàm số y = f (x) = - 3x . Hai điểm M, N thuộc đồ thị hàm số
Đáp án: D Phương pháp giải: Áp dụng thay tọa độ một điểm vào hàm số để tìm tọa độ còn lại; dạng đồ thị hàm số y = ax. Lời giải chi tiết: Nếu M có hoành độ là -1 thì tung độ của điểm M là y = -3.(-1) = 3. Nếu N có tung độ là 2 thì hoành độ của điểm N là \(2=-3.x\Rightarrow x=-\frac{2}{3}\) Do M, N thuộc đồ thị hàm số y = -3x nên đường thẳng MN đi qua gốc tọa độ O Chọn D. Câu hỏi 8 : Cho điểm A (a; - 0,2 ) thuộc đồ thị hàm số y = 4x . Ta có :
Đáp án: B Phương pháp giải: Áp dụng thay một tọa độ đã biết vào hàm số để tìm tọa độ còn lại. Lời giải chi tiết: Do điểm A (a; - 0,2 ) thuộc đồ thị hàm số y = 4x nên ta có :\(-0,2=4.a\Rightarrow a=-0,2:4=-0,05\). Chọn B. Câu hỏi 9 : Cho \(f\left( x \right)=-2\text{x+2}\); \(g\left( x \right)=3x+1\) a) Tính \(P=2f\left( 2 \right)+3g\left( 3 \right)\) b) Tìm \(A\left( -\frac{1}{2};a \right)\) thuộc đồ thị hàm số \(f\left( x \right)\) c) Tìm \(B\left( b;-6 \right)\) thuộc đồ thị hàm số \(g\left( x \right)\) d) Tìm \(M\left( {{x}_{0}};{{y}_{0}} \right)\) biết \(N\left( {{x}_{0}};2 \right)\) thuộc đồ thị hàm số \(f\left( x \right)\), \(P\left( 3;{{y}_{0}} \right)\) thuộc đồ thị hàm số \(g\left( x \right)\)
Đáp án: A Phương pháp giải: a) Thay các giá trị để tính giá trị biểu thức b,c,d) Thay các tọa độ có sẵn vào hàm số để tìm các tọa độ còn lại, từ đó suy ra điểm cần tìm. Lời giải chi tiết: a) \(P=2f\left( 2 \right)+3g\left( 3 \right)=2.\left( -2.2+2 \right)+3.\left( 3.3+1 \right)=2.(-2)+3.10=-4+30=26\) Vậy \(P = 26\). b) Do \(A\left( -\frac{1}{2};a \right)\) thuộc đồ thị hàm số \(f\left( x \right)\) nên \(x=-\frac{1}{2};\,\,y=a\). Thay \(x=-\frac{1}{2};\,\,y=a\) vào \(f\left( x \right)\)ta được: \(a=2.\frac{-1}{2}+2=1\). Vậy \(A\left( -\frac{1}{2};1 \right)\). c) Do \(B\left( b;-6 \right)\) thuộc đồ thị hàm số \(g\left( x \right)\) nên\(x=b;\,\,y=-6\). Thay \(x=b;\,\,y=-6\) vào \(g\left( x \right)\)ta có: \(-6=3.b+1\Leftrightarrow 3b=-7\Leftrightarrow b=\frac{-7}{3}\) Vậy \(B\left( \frac{-7}{3};-6 \right)\). d) Do \(N\left( {{x}_{0}};2 \right)\) thuộc đồ thị hàm số \(f(x)\) nên \(x={{x}_{0}};\,\,y=2\). Thay \(x={{x}_{0}};\,\,y=2\) vào \(f(x)\)ta được. \(2=-2.{{x}_{0}}+2\Leftrightarrow {{x}_{0}}=0\) Do \(P\left( 3;{{y}_{0}} \right)\)thuộc đồ thị hàm số\(g\left( x \right)\) nên \(x=3,\,y={{y}_{0}}\). Thay \(x=3,\,y={{y}_{0}}\) vào \(g\left( x \right)\)ta được \({{y}_{0}}=3.3+1=10\). Vậy \(M\left( 0\,\,;\,10 \right)\). Chọn A. Câu hỏi 10 : Nếu y = f(x) = 2x thì f(3) = ?
Đáp án: C Phương pháp giải: Thay x = 3 vào y = f(x) để tính f(3). Lời giải chi tiết: \(f(3)=2.3=6\).Vậy f(3) = 6. Chọn C.
Câu hỏi 11 : Cho hàm số \(y=f(x)=-2x\). Đáp án nào sau đây sai?
Đáp án: B Phương pháp giải: Thay lần lượt các giá trị của x vào để kiểm tra. Lời giải chi tiết: Thay các đáp án ta thấy \(f\left( \frac{1}{2} \right)=-2.\frac{1}{2}=-1\ne 1\). Do đó \(f\left( \frac{1}{2} \right)=1\) là sai. Chọn B Câu hỏi 12 : Một người đi bộ với vận tốc đều 5 km/h. a. Hãy biểu diễn quãng đường y (km) người đó đi được thời gian x (giờ) b. Vẽ đồ thị hàm số đó. c. Từ đồ thị hàm số hãy cho biết trong 2 giờ người đó đi được bao nhiêu km?
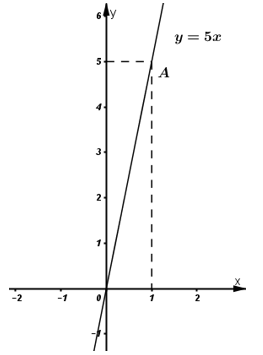
Đáp án: B Phương pháp giải: a) Áp dụng công thức: Quãng đường = vận tốc x thời gian. b) Dựa vào cách vẽ đồ thị hàm số y = ax. c) Thay x = 2 vào hàm số đã xác định ở câu a để suy ra quãng đường cần tìm. Lời giải chi tiết:
a) Quãng và thời gian người đó đi hết quãng đường là hai đại lượng tỉ lể thuận. Ta có công thức : Quãng đường = vận tốc x thời gian. Vậy ta có biểu diễn y theo x là : y = 5x b) Vẽ đồ thị hàm số y = 5x Đồ thị y = 5x là đường thẳng OA đi qua 2 điểm O(0;0) và A(1; 5). c) Từ đồ thị y = 5x ta có khi x = 2 thì y = 10 Trong 2h người đó đi được 10 km. Chọn B Câu hỏi 13 : Tìm hệ số tỉ lệ trong các bài tập sau Câu 1: Cho y tỉ lệ thuận với x, biết \(x = - 8\) thì \(y = \frac{2}{3}\). Tính hệ số tỉ lệ k.
Đáp án: A Phương pháp giải: Vận dụng lý thuyết tỉ lệ thuận, tỉ lệ nghịch. Lời giải chi tiết: Vì y tỉ lệ thuận với \(x \Rightarrow k = \frac{y}{x} = \frac{2}{{3.\left( { - 8} \right)}} = - \frac{1}{{12}}\) Câu 2: Cho y tỉ lệ nghịch với x, biết \(x = \frac{{ - 4}}{3}\) thì \(y = - 12\). Tính hệ số tỉ lệ a.
Đáp án: B Phương pháp giải: Vận dụng lý thuyết tỉ lệ thuận, tỉ lệ nghịch. Lời giải chi tiết: Vì y tỉ lệ nghịch với \(x \Rightarrow a = x.y = \frac{{ - 4}}{3}.\left( { - 12} \right) = 16\) Câu hỏi 14 : Cho x và y tỉ lệ thuận với nhau và khi \(x = - 3\) thì \(y = 12\). Hệ số tỉ lệ k của y đối với x là
Đáp án: B Phương pháp giải: Cho x và y tỉ lệ thuận với nhau thì hệ số tỉ lệ k của y đối với x là \(\frac{y}{x}\)
Lời giải chi tiết: x và y tỉ lệ thuận với nhau \( \Rightarrow k = \frac{y}{x} = \frac{{12}}{{ - 3}} = - 4\) Chọn B Câu hỏi 15 : Cho hàm số \(y = f\left( x \right) = x + 3.\) Khẳng định nào sau đây là Sai?
Đáp án: C Phương pháp giải: Xét tính đúng sai của các đáp án đã cho. Lời giải chi tiết: \(f\left( 1 \right) = 1 + 3 = 4 \Rightarrow A\) đúng. \(f\left( 0 \right) = 0 + 3 = 3 \Rightarrow B\) đúng. \(f\left( { - 1} \right) = - 1 + 3 = 2 \ne 4 \Rightarrow C\)sai. \(f\left( 5 \right) = 5 + 3 = 8 \Rightarrow D\) đúng. Chọn C Câu hỏi 16 : Giá trị của hàm số \(y = f\left( x \right) = 3{x^2} + 2\) tại \(x = - 1\) bằng:
Đáp án: D Phương pháp giải: Thay \(x = - 1\) vào hàm số đã cho rồi tính toán Lời giải chi tiết: Thay \(x = - 1\) vào hàm số \(y = f\left( x \right) = 3{x^2} + 2\) ta được: \(f\left( { - 1} \right) = 3.{\left( { - 1} \right)^2} + 2 = 5\) Chọn D Câu hỏi 17 : Điểm nào sau đây thuộc đồ thị hàm số \(y = 4x\)?
Đáp án: A Phương pháp giải: Thay tọa độ các điểm vào hàm số đã cho để xác định điểm thuộc đồ thị Lời giải chi tiết: Thay \(x = \frac{1}{3};y = \frac{4}{3}\) vào hàm số \(y = 4x\) ta được: \(\frac{4}{3} = 4.\frac{1}{3} \Leftrightarrow \frac{4}{3} = \frac{4}{3}\) (luôn đúng) Nên điểm có tọa độ \(\left( {\frac{1}{3};\frac{4}{3}} \right)\) thuộc đồ thị hàm số \(y = 4x.\) Chọn A Câu hỏi 18 : Điểm M(-2; 3) không thuộc đồ thị hàm số:
Đáp án: D Phương pháp giải: Thay tọa độ điểm M vào các hàm đố, M không thỏa mãn hàm số nào thì M không thuộc đồ thị hàm số đó. Lời giải chi tiết: Thay M(-2; 3) đồ thị hàm số \(y=-x+5\) ta được: \(3\ne -(-2)+5=7\). Do đó M không thuộc đồ thị hàm số \(y=-x+5\) Chọn D. Câu hỏi 19 : Cho \(y=\frac{50}{x}\) và x = 10, giá trị tương ứng của y bằng:
Đáp án: B Phương pháp giải: Thay x vào hàm số đã cho để tính giá trị của y. Lời giải chi tiết: Thay x = 10 vào \(y=\frac{50}{x}\) ta được: \(y=\frac{50}{10}=5\). Vậy y = 5. Chọn B. Câu hỏi 20 : Một đoạn dây thép dài 6m nặng 75gam. Để bán 100m dây thép thì người bán cần phải cân cho khách hàng bao nhiêu gam?
Đáp án: D Phương pháp giải: Áp dụng tính chất của tỉ lệ thuận: \(\frac{{{x_1}}}{{y_1}} = \frac{{{x_2}}}{{{y_2}}}.\) Lời giải chi tiết: Số mét dây thép và cân nặng của dây thép là hai đại lượng tỉ lệ thuận. Gọi cân nặng của 100m dây thép là \(x\,\,\,\left( gam \right),\,\,\,\left( x>75 \right).\) Khi đó áp dụng tính chất của tỉ lệ thuận ta có: \(\frac{6}{75}=\frac{100}{x}\Rightarrow x=\frac{100.75}{6}=1250\,\,\,\left( gam \right).\) Vậy để bán 100m dây thép thì người bán cần phải cân cho khách hàng \(1250\) gam dây thép. Chọn D.
|
