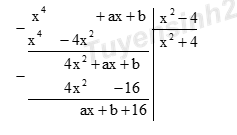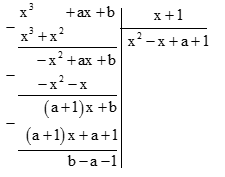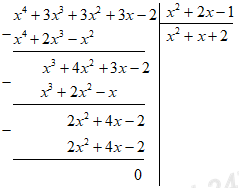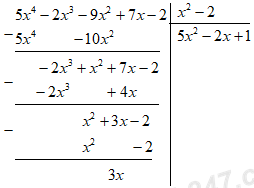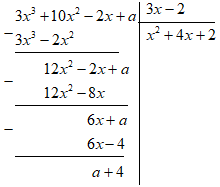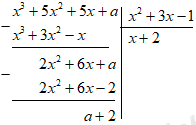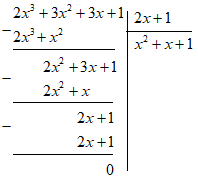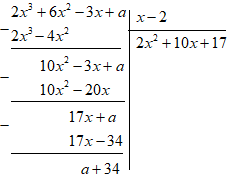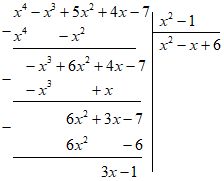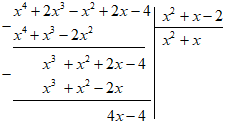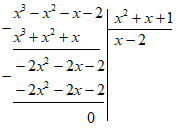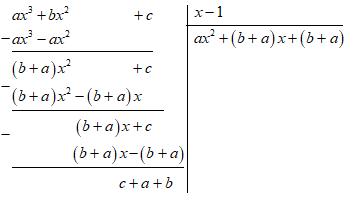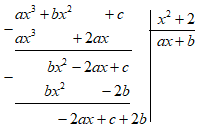15 bài tập vận dụng Chia đa thức 1 biến đã sắp xếpLàm bàiCâu hỏi 1 : Xác định hằng số a và b sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\)
Đáp án: A Phương pháp giải: - Đặt phép chia. - Để phép chia hết thì số dư cuối cùng phải bằng 0, từ đó ta tìm ra a và b Lời giải chi tiết: Để \({x^4} + ax + b\) chia hết cho \({x^2} – 4\) thì \(ax + b + 16 = 0 \Leftrightarrow \left\{ \matrix{ax = 0 \hfill \cr b + 16 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = 0 \hfill \cr b = - 16 \hfill \cr} \right.\) Chọn A. Câu hỏi 2 : Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư 2 :
Đáp án: D Phương pháp giải: - Đặt phép chia. - Để phép chia có dư thì số dư cuối cùng phải bằng giá trị dư của biểu thức, từ đó ta tìm ra . Lời giải chi tiết: Để \(6{x^3} - 7{x^2} - x + a\) chia 2x + 1 dư 2 thì \(a - 2 = 2 \Leftrightarrow a = 4\) Câu hỏi 3 : Không thực hiện phép chia hãy xét xem đa thức có chia hết cho đa thức hay không? \(A = {x^3} + 12x + 6{x^2} + 8\) \(B = {\left( {x + 2} \right)^2}\) Phương pháp giải: - Phân tích biểu thức A thành tích các đa thức (sử dụng hằng đẳng thức). - Nếu A là tích các đa thức giống đa thức B thì A chia hết cho B. Lời giải chi tiết: Ta có: \(\eqalign{& A = {x^3} + 12x + 6{x^2} + 8 = {x^3} + 3.2.{x^2} + {3.2^2}.x + {2^3} = {\left( {x + 2} \right)^3} \cr & B = {\left( {x + 2} \right)^2} \cr} \) Vậy đa thức A chia hết cho đa thức B. Câu hỏi 4 : Tìm các hằng số a và b sao cho \(\left( {{x^3} + ax + b} \right):\left( {x + 1} \right)\) dư 7 và \(\left( {{x^3} + ax + b} \right):\left( {x - 3} \right)\) dư (- 5)
Đáp án: B Phương pháp giải: - Đặt phép chia. - Để phép chia có dư theo điều kiện đề bài thì số dư cuối cùng phải bằng số dư đề bài cho. Từ đó ta được phương trình thứ nhất. - Thực hiện tương tự, được phương trình thứ hai. Lập hệ phương trình, giải hệ thu được giá trị của a và b. Lời giải chi tiết: Để \({x^3} + ax + b\) chia cho x + 1 dư 7 thì \(b - a - 1 = 7 \Leftrightarrow - a + b = 8\;(1)\) Để \({x^3} + ax + b\) chia cho x - 3 dư - 5 thì \(b + 3a + 27 = -5 \Leftrightarrow 3a + b = - 32\;(2)\) Từ (1) và (2) ta có hệ \(\left\{ \matrix{- a + b = 8 \hfill \cr 3a + b = - 32 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = - 10 \hfill \cr b = - 2 \hfill \cr} \right.\) Câu hỏi 5 : Tìm đa thức bị chia biết đa thức chia là \(2{x^2} + x + 1\), thương là \({x^2} + 2\), dư là \(2x + 1\)
Đáp án: D Phương pháp giải: Đa thức bị chia = Đa thức chia x Đa thức thương + Đa thức dư. Lời giải chi tiết: Đa thức bị chia A là: \(\begin{array}{l}\left( {2{x^2} + x + 1} \right)\left( {{x^2} + 2} \right) + 2x + 1\\ = 2{x^4} + 4{x^2} + {x^3} + 2x + {x^2} + 2 + 2x + 1\\ = 2{x^4} + {x^3} + 5{x^2} + 4x + 3\end{array}\) Chọn D. Câu hỏi 6 : Kết quả của phép chia: Câu 1: \(\left( {{x^4} + 3{x^3} + 3{x^2} + 3x - 2} \right):\left( {{x^2} + 2x - 1} \right)\)
Đáp án: C Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Lời giải chi tiết: Chọn C. Câu 2: \(\left( {5{x^4} - 2{x^3} - 9{x^2} + 7x - 2} \right):\left( {{x^2} - 2} \right)\)
Đáp án: B Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Lời giải chi tiết: Chọn B. Câu hỏi 7 : Tìm đa thức bị chia biết đa thức chia là \({x^2} + 2x + 5\), thương là \({x^2} + 2\), dư là \(2x - 1\)
Đáp án: A Phương pháp giải: Đa thức bị chia = Đa thức chia x Đa thức thương + Đa thức dư. Lời giải chi tiết: Đa thức bị chia A là: \(\begin{array}{l}\left( {{x^2} + 2x + 5} \right)\left( {{x^2} + 2} \right) + 2x - 1\\ = {x^4} + 2{x^2} + 2{x^3} + 4x + 5{x^2} + 10 + 2x - 1\\ = {x^4} + 2{x^3} + 7{x^2} + 6x + 9\end{array}\) Chọn A. Câu hỏi 8 : Tìm \(a\) để \(3{x^3} + 10{x^2} - 2x + a\) chia hết cho \(3x - 2\)
Đáp án: B Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Phép chia hết có dư bằng 0. Từ đó, ta giải tìm \(a.\) Lời giải chi tiết: Để \(3{x^3} + 10{x^2} - 2x + a\) chia hết cho \(3x - 2\) thì \(a + 4 = 0 \Leftrightarrow a = - 4\) Chọn B. Câu hỏi 9 : Tìm \(a\) để \({x^3} + 5{x^2} + 5x + a\) chia hết cho \({x^2} + 3x - 1\)
Đáp án: C Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Phép chia hết có dư bằng 0. Từ đó, ta giải ra \(a.\) Lời giải chi tiết: Để \({x^3} + 5{x^2} + 5x + a\) chia hết cho \({x^2} + 3x - 1\) thì \(a + 2 = 0 \Leftrightarrow a = - 2\) Chọn C. Câu hỏi 10 : Kết quả của phép chia \(\left( {2{x^3} + 3{x^2} + 3x + 1} \right):\left( {2x + 1} \right)\) là
Đáp án: C Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Lời giải chi tiết: Chọn C. Câu hỏi 11 : Tìm \(a\) để \(2{x^3} + 6{x^2} - 3x + a\) chia hết cho \(x - 2\)
Đáp án: A Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Phép chia hết có số dư bằng 0. Từ đó, ta giải phương trình để tìm \(a\) Lời giải chi tiết: Để \(2{x^3} + 6{x^2} - 3x + a\) chia hết cho \(x - 2\) thì \(a + 34 = 0 \Leftrightarrow a = - 34\) Chọn A. Câu hỏi 12 : Thực hiện phép chia Câu 1: \(\left( {{x^4} - {x^3} + 5{x^2} + 4x - 7} \right):\left( {{x^2} - 1} \right)\)
Đáp án: D Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Lời giải chi tiết: Chọn D. Câu 2: \(\left( {{x^4} + 2{x^3} - {x^2} + 2x - 4} \right):\left( {{x^2} + x - 2} \right)\)
Đáp án: C Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Lời giải chi tiết: Chọn C. Câu hỏi 13 : Thực hiện phép chia \(\left( {{x^3} - {x^2} - x - 2} \right):\left( {{x^2} + x + 1} \right)\)
Đáp án: B Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Lời giải chi tiết: Hay \({x^3} - {x^2} - x - 2 = \left( {{x^2} + x + 1} \right)\left( {x - 2} \right)\) Chọn B. Câu hỏi 14 : \(P = {{2{n^3} - 3{n^2} + 3n - 1} \over {n - 1}}\) Tìm \(n \in Z\) để \(P \in Z\)
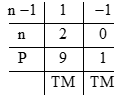
Đáp án: A Phương pháp giải: - Đặt phép chia. - Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia. Suy ra, số chia là ước của số dư cuối cùng. - Lập bảng thử chọn để chọn ra giá trị của thỏa mãn. Lời giải chi tiết: \(2{n^3} - 3{n^2} + 3n - 1 = \left( {2{n^2} - n + 2} \right)\left( {n - 1} \right) + 1\) Để \(2{n^3} - 3{n^2} + 3n – 1\) chia hết cho n - 1 thì 1 chia hết cho n - 1. \( \Rightarrow \left( {n - 1} \right) \in \left\{ {1, - 1} \right\}\) vậy \(n = \left\{ {0,2} \right\}\) để \(P \in Z\)
Câu hỏi 15 : Tìm \(a,\,\,b,\,\,c\) để \(a{x^3} + b{x^2} + c\) chia hết cho \(x - 1\), chia cho \({x^2} + 2\) thì dư \( - 2x + 1\)
Đáp án: D Phương pháp giải: Thực hiện phép chia đa thức một biến đã sắp xếp. Phép chia hết có dư bằng 0. Từ đó, ta có 1 phương trình. Phép chia có dư, đồng nhất hệ số với \( - 2x + 1\) ta được 2 phương trình. Giải hệ 3 phương trình 3 ẩn ta được \(a,\,\,b,\,\,c.\) Lời giải chi tiết: Để \(a{x^3} + b{x^2} + c\) chia hết cho \(x - 1\) thì \(a + b + c = 0\,\,\,\,\left( 1 \right)\) Để \(a{x^3} + b{x^2} + c\) chia cho \({x^2} + 2\) dư \( - 2x + 1\) thì \( - 2ax + 2b + c = - 2x + 1\,\) \( \Leftrightarrow \left\{ \begin{array}{l} - 2a = - 2\\2b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\2b + c = 1\end{array} \right.\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right);\,\,\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}a = 1\\1 + b + c = 0\\2b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = - 1 - b\\2b - 1 - b = 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = - 1 - b\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = - 3\end{array} \right.\) Vậy \(\left\{ \begin{array}{l}a = 1\\b = 2\\c = - 3\end{array} \right.\) hay đa thức bị chia là \({x^3} + 2{x^2} - 3.\) Chọn D.
|