30 bài tập con lắc lò xo mức độ vận dụng caoLàm bàiCâu hỏi 1 : Một vật có khối lượng m = 1kg được treo vào lò xo độ cứng 100N/m, một đầu lò xo được giữ cố định. Ban đầu vật được đặt ở vị trí lò xo không biến dạng và đặt lên một miếng ván nằm ngang. Sau đó người ta cho miếng vãn chuyển động nhanh dần đều thẳng đứng xuống dưới với gia tốc a = 2m/s2. Lấy g = 10m/s2. Sau khi rời tấm ván vật dao động điều hòa với vận tốc cực đại là
Đáp án: A Phương pháp giải: Áp dụng định luật II niuton và lí thuyết về dao động điều hoà Lời giải chi tiết: Đáp án A Viết phương trình 2 Niuton cho vật nặng ta được: P – N – Fđh = ma Khi vật bắt đầu rời tấm ván thì N = 0. Khi đó P – Fdh = ma => mg - k = ma => ∆l = 0,08m = 8cm Với chuyển động nhanh dần đều có vận tốc đầu bằng 0 ta áp dụng công thức: \(s = \Delta \ell = {1 \over 2}a{t^2} \Rightarrow t = \sqrt {0,08} (s)\) Vận tốc khi rời khỏi ván là: v = at = 2\(\sqrt {0,08} \) m/s Ta có ω = 10 rad/s , vị trí cân bằng của vật lò xo dãn \(\Delta {\ell _0} = mg/k = 0,1m = 10cm\) Tại thời điểm vật rời ván ta có: x = - 0,02m; v = 2\(\sqrt {0,08} \) m/s Biên độ dao động: \({A^2} = {x^2} + {{{v^2}} \over {{\omega ^2}}}\) => A = 0,06m = 6cm Vận tốc cực đại của vât: v0 = ωA = 60cm/s Câu hỏi 2 : Con lắc lò xo gồm lò xo có độ cứng 200N/m , quả cầu m có khối lượng 1kg đang dao động điều hòa theo phương thẳng đứng với biên độ 12,5cm. Khi quả cầu xuống đến vị trí thấp nhất thì có một vật nhỏ khối lượng 500g bay theo phương trục lò xo, từ dưới lên với tốc độ 6m/s tới dính chặt vào M. Lấy g = 10m/s2. Sau va chạm , hai vật dao động điều hòa. Biên độ dao động của hệ hai vật sau và chạm là :
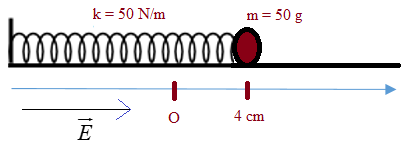
Đáp án: B Phương pháp giải: Áp dụng định luật bảo toàn động lượng Lời giải chi tiết: Đáp án B Ở vị trí cân bằng lò xo dãn một đoạn ∆l . Ta có \(k\Delta \ell = mg \Rightarrow \Delta \ell = 0,05m = 5cm\) Khi quả cầu đến vị trí thấp nhất thì lò xo đang dãn đoạn A + ∆l = 12,5+5=17,5cm và vận tốc của vật bằng 0. Sau khi va chạm vận tốc hai vật là: mv = (m+M)v’ => 0,5.6 = 1,5.v’ => v’ = 2m/s. Sau đó hai vật dao động điều hòa, vị trí cân bằng lò xo dãn ∆l' với \(k\Delta \ell ' = (m + M)g \Rightarrow \Delta \ell ' = 0,075m = 7,5cm\) Vậy khi x = 10cm, v’ = 2m/s, \(\omega ' = \sqrt {{k \over {M + m}}} = \sqrt {{{400} \over 3}} rad/s\) Áp dụng công thức độc lập: \({A^2} = {x^2} + {{{v^2}} \over {{\omega ^2}}} \Rightarrow A = 0,2m = 20cm\) Câu hỏi 3 : Một con lắc lò xo ngang có độ cứng k = 50 N/m nặng 200g. Bỏ qua ma sát giữa vật và mặt phẳng ngang. Khi vật đang ở vị trí cân bằng thì tác dụng vào vật một lực không đổi 2N theo dọc trục của lò xo. Tốc độ của vật sau 2/15s
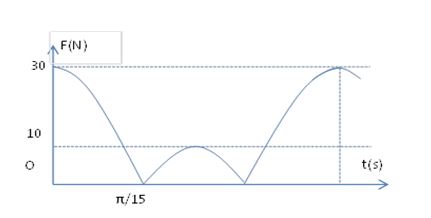
Đáp án: B Phương pháp giải: Áp dụng hệ thức độc lập với thời gian của x và v Lời giải chi tiết: Đáp án B Vật dao động điều hòa với chu kỳ \(T = 2\pi \sqrt {{m \over k}} \) = 0,4s, Vật đang ở vị trí cân bằng thì tác dụng lực, vậy vị trí cân bằng mới là vị trí lò xo biến dạng một đoạn Giả sử lực tác dụng hướng sang phải, vậy thời điểm ban đầu vật ở biên bên trái. PT dao động: x = 4cos(5πt+π)cm, sau 2/15s vật có x = 2cm. AD công thức độc lập: \({A^2} = {x^2} + {{{v^2}} \over {{\omega ^2}}}\) ta tìm được tốc độ của vật là 54cm/s Câu hỏi 4 : Một con lắc lò xo đặt nằm ngang gồm vật M có khối lượng 400 g và lò xo nhẹ có hệ số đàn hồi 40N/m đang dao động điều hòa xung quanh vị trí cân bằng với biên độ 5 cm. Khi vật M qua vị trí cân bằng người ta thả nhẹ vật m có khối lượng 100 g lên M (m dính chặt ngay vào M), sau đó hệ m và M dao động điều hòa với biên độ
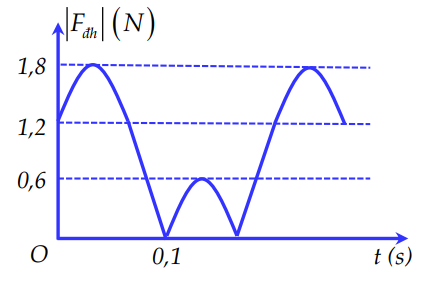
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B Câu hỏi 5 : Một con lắc lò xo treo thẳng đứng tại nơi có g =10m/s2 đang dao động điều hòa trên trục Ox thẳng đứng hướng lên. Cho đồ thị biểu diễn độ lớn của lực đàn hồi lò xo vào thời gian như hình vẽ. Độ cứng lò xo và khối lượng vật nặng lần lượt bằng
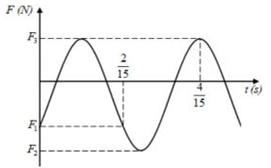
Đáp án: A Phương pháp giải: Lời giải chi tiết: Câu hỏi 6 : Một con lắc lò xo gồm một vật nhỏ có khối lượng m = 200 g và lò xo có độ cứng k, đang dao động điều hòa theo phương thẳng đứng. Chọn gốc tọa độ ở vị trí cần bằng, chiều dương hướng xuống dưới. Đồ thị biểu diễn sự phụ thuộc của lực đàn hồi theo thời gian được cho như hình vẽ. Biết F1 + 3F2+ 6F3 = 0. Lấy g =10 m/s2. Tỉ số thời gian lò xo giãn với thời gian lò xo nén trong một chu kì gần giá trị nào nhất sau đây?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Từ đồ thị ta thấy: Lực đàn hồi tại thời điểm ban đầu: F = F1 = - k(Δl0 + x) Lực đàn hồi tại vị trí biên dương: F = F2 = - k(Δl0 + A) Lực đàn hồi tại vị trí biên âm: F = F3 = - k(Δl0 – A) Gọi Δt là thời gian từ t = 0 đến t = 2/15s Ta có: \(T + \frac{{\Delta t}}{2} = 2\Delta t \Rightarrow \Delta t = \frac{{2T}}{3} \Rightarrow x = \frac{A}{2}\) Theo đề bài: \({F_1} + 3{F_2} + 6{F_3} = 0 \Leftrightarrow k\left( {\Delta {l_0} + x} \right) + 3k\left( {\Delta {l_0} + A} \right) + 6k\left( {\Delta {l_0}--A} \right) = 0 \Rightarrow \Delta {l_0} = 0,25A\) => Thời gian lo xo nén là : \({t_n} = \frac{{2\alpha }}{{360}}T = \frac{{151}}{{360}}T = 0,42T \Rightarrow {t_g} = T--{t_n} = 0,58T\) Tỉ số thời gian giãn và nén trong một chu kì: \(\frac{{{t_g}}}{{{t_n}}} = \frac{{0,58}}{{0,42}} = 1,381\) => Chọn B Câu hỏi 7 : Một con lắc lò xo dao động điều hoà trên mặt phẳng ngang với chu kỳ T = 2π (s). Khi con lắc đến vị trí biên dương thì một vật có khối lượng m chuyển động cùng phương ngược chiều đến va chạm đàn hồi xuyên tâm với con lắc. Tốc độ chuyển động của m trước va chạm là 5cm/s và sau va chạm vật m bật ngược trở lại với vận tốc là 3cm/s. Gia tốc của vật nặng của con lắc ngay trước va chạm là –2 cm/s2. Sau va chạm con lắc đi được quãng đường bao nhiêu thi đổi chiều chuyển động?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Câu hỏi 8 : Một con lắc lò xo treo thẳng đứng gồm hai vật m1 = m2 = 0,5 kg được dính với nhau, m1 được gắn vào lò xo k = 100N/m. Lúc đầu hệ dao động với biên độ A = 5cm. Khi hệ qua vị trí cân bằng thì m2 bị tách ra. Biên độ dao động mới của hệ là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Câu hỏi 9 : Một con lắc lò xo nằm ngang gồm vật nhỏ có khối lượng m = 250g và lò xo có độ cứng k = 100 N/m. Bỏ qua ma sát. Ban đầu, giữ vật ở vị trí lò xo nén 1 cm. Buông nhẹ vật, đồng thời tác dụng vào vật một lực F = 3N không đổi có hướng dọc theo trục lò xo và làm lò xo giãn. Sau khoảng thời gian Δt = π/40 (s) thì ngừng tác dụng F. Vận tốc cực đại của vật sau đó bằng
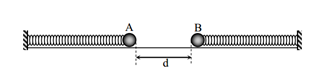
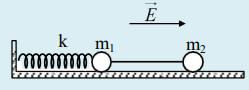
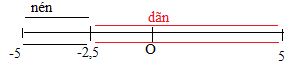
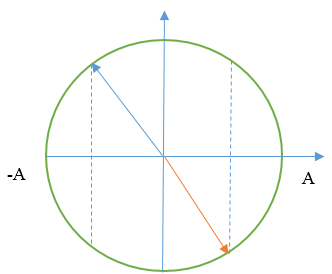
Đáp án: D Phương pháp giải: Lời giải chi tiết: Câu hỏi 10 : Trên mặt phẳng nằm ngang có hai con lắc lò xo. Các vật nhỏ A và B có khối lượng như nhau; các lò xo có cùng chiều dài tự nhiên, có độ cứng kB = 4kA. Khi ở vị trí cân bằng, hai vật cách nhau một khoảng là d. Ban đầu, A và B được giữ ở vị trí sao cho lò xo gắn với A bị dãn 4 cm còn lò xo gắn với B bị nén 4 cm. Đồng thời thả nhẹ để hai vật dao động điều hòa trên cùng một đường thẳng (hình vẽ). Để khi dao động hai vật A và B không bao giờ va vào nhau thì khoảng cách d nhỏ nhất phải gần nhất với giá trị nào sau đây?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Câu hỏi 11 : Tiến hành thí nghiệm với 2 con lắc lò xo A và B có quả nặng và chiều dài tự nhiên giống nhau với độ cứng lần lượt là k và 2k. Hai con lắc được treo thẳng đứng vào cùng một giá đỡ. Kéo hai quả nặng đến cùng một vị trí ngang nhau rồi thả nhẹ cùng lúc. Năng lượng dao động của con lắc B gấp 8 lần năng lượng dao động của con lắc A. Gọi tA, tBlà khoảng thời gian ngắn nhất kể từ lúc bắt đầu thả hai vật đến khi lực đàn hồi của mỗi con lắc có độ lớn nhỏ nhất. Tỷ số \(\frac{{{t_B}}}{{{t_A}}}\) là:
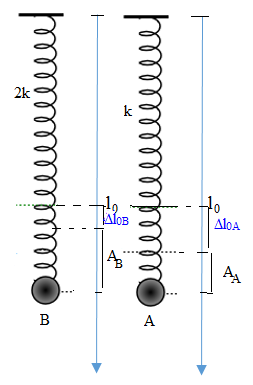
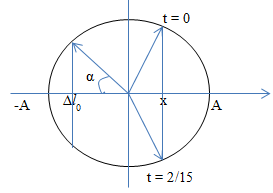
Đáp án: A Phương pháp giải: Xác định độ dãn ban đầu của mỗi lò xo: \(\Delta {l_0} = \frac{{mg}}{k}\) Áp dụng công thức cơ năng \({\rm{W}} = \frac{1}{2}.k.{A^2}\) Lực đàn hồi: \(F = k.\left| {\Delta l} \right|\) Chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \) Sử dụng VTLG để xác định thời gian từ vị trí ban đầu đến vị trí lò xo không dãn và tìm tỉ số. Lời giải chi tiết:
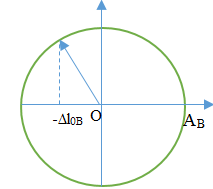
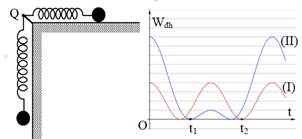
Độ dãn ban đầu của lò xo A là \(\Delta {l_{0A}} = \frac{{mg}}{k}\) Độ dãn ban đầu của lò xo B là \(\Delta {l_{0B}} = \frac{{mg}}{{2k}} = \frac{1}{2}\Delta {l_{0A}}\) Áp dụng công thức cơ năng: \(\left\{ \begin{array}{l} Từ hình vẽ ta thấy: \(\begin{array}{l} Chu kì dao động của con lắc lò xo A: \({T_A} = 2\pi \sqrt {\frac{m}{k}} \) Chu kì dao động của con lắc lò xo B: \({T_B} = 2\pi \sqrt {\frac{m}{{2k}}} = \frac{{{T_A}}}{{\sqrt 2 }}\) Ta thấy biên độ của A nhỏ hơn độ dãn ban đầu của lò xo, vì vậy lực đàn hồi của lò xo luôn lò là lực kéo và có giá trị nhỏ nhất tại biên âm. Ban đầu vật ở biên dương, nên \({t_A} = \frac{{{T_A}}}{2}\) Lò xo B có biên độ lớn hơn độ dãn ban đầu, nên lực đàn hồi nhỏ nhất = 0 tại vị trí lò xo không dãn. Ta có VTLG:
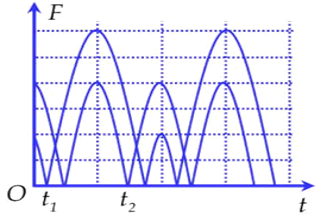
Thời gian: \({t_B} = \frac{{\frac{\pi }{2} + {\rm{ar}}\cos \frac{{\Delta {l_B}}}{{{A_B}}}}}{{2\pi }}.{T_B} = \frac{{{T_B}}}{3} = \frac{{{T_A}}}{{3\sqrt 2 }}\) Ta có tỉ số: \(\frac{{{t_B}}}{{{t_A}}} = \frac{{\frac{{{T_A}}}{{3\sqrt 2 }}}}{{\frac{{{T_A}}}{2}}} = \frac{{\sqrt 2 }}{3}\) Chọn A. Câu hỏi 12 : Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng 80 cm và đầu cố định gắn chung tại điểm Q. Con lắc (I) nằm ngang trên mặt bàn nhẵn. Con lắc (II) treo thẳng đứng cạnh mép bàn như hình vẽ. Kích thích cho hai con lắc dao động điều hòa tự do. Chọn mốc thế năng đàn hồi của mỗi con lắc tại các vị trí tương ứng của vật lúc lò xo có chiều dài tự nhiên. Thế năng đàn hồi các con lắc phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ. Biết tại thời điểm t = 0, cả hai lò xo đều dãn và t2 – t1 = \(\dfrac{\pi }{{12}}\)s. Lấy g = 10 m/s2. Tại thời điểm t = \(\dfrac{\pi }{{10}}\,s\), khoảng cách hai vật dao động gần nhất với giá trị nào sau đây ?
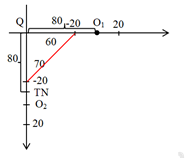
Đáp án: D Phương pháp giải: Cơ năng của con lắc lò xo nằm ngang: \({\rm{W}} = \dfrac{1}{2}k{A^2}\) Cơ năng tại vị trí thấp nhất và cao nhất của con lắc lò xo thẳng đứng: \(\left\{ \begin{array}{l}{{\rm{W}}_1} = \dfrac{1}{2}k{\left( {A - \Delta l} \right)^2}\\{{\rm{W}}_2} = \dfrac{1}{2}k{\left( {A + \Delta l} \right)^2}\end{array} \right.\) Sử dụng kĩ năng đọc đồ thị Chu kì của con lắc lò xo treo thẳng đứng: \(T = 2\pi \sqrt {\dfrac{{\Delta l}}{g}} \) Khoảng cách giữa hai con lắc: \(d = \sqrt {{x_1}^2 + {x_2}^2} \) Lời giải chi tiết: Con lắc (1) ứng với đồ thị (I) Tại thời điểm t = 0, \({{\rm{W}}_1}\max \Rightarrow \) lò xo đang giãn, vật ở vị trí biên dương \( \Rightarrow {t_2} = \dfrac{T}{2} + \dfrac{T}{4} = \dfrac{{3T}}{4}\) Con lắc thứ (2) ứng với đồ thị (II) \({{\rm{W}}_2}\max \Leftrightarrow \) vật ở biên dưới \(\begin{array}{l} \Rightarrow \dfrac{{\dfrac{1}{2}k{{\left( {{A_2} + \Delta l} \right)}^2}}}{{\dfrac{1}{2}k{{\left( {{A_2} - \Delta l} \right)}^2}}} = 9 \Rightarrow \dfrac{{{A_2} + \Delta l}}{{{A_2} - \Delta l}} = 3\\ \Rightarrow 3{A_2} - 3\Delta l = {A_2} + \Delta l \Rightarrow 2{A_2} = 4\Delta l \Rightarrow \Delta l = \dfrac{{{A_2}}}{2}\\ \Rightarrow {t_1} = \dfrac{T}{4} + \dfrac{T}{{12}} = \dfrac{T}{3}\\ \Rightarrow \dfrac{{3T}}{4} - \dfrac{T}{3} = \dfrac{\pi }{{13}} \Rightarrow \dfrac{{5T}}{{12}} = \dfrac{\pi }{{12}} \Rightarrow T = \dfrac{\pi }{5}\,\,\left( s \right)\end{array}\) Ta có: \(T = 2\pi \sqrt {\dfrac{{\Delta l}}{g}} \Rightarrow \dfrac{\pi }{5} = 2\pi \sqrt {\dfrac{{\Delta l}}{{10}}} \Rightarrow \Delta l = 0,1\,\,\left( m \right) = 10\,\,\left( {cm} \right)\) \( \Rightarrow {A_2} = 2\Delta l = 20\,\,\left( {cm} \right)\) Ta có:\(\dfrac{{{{\rm{W}}_{1\max }}}}{{{{\rm{W}}_{2\max }}}} = \dfrac{{\dfrac{1}{2}k{A_1}^2}}{{\dfrac{1}{2}k{{\left( {{A_2} + \Delta l} \right)}^2}}} = \dfrac{4}{9} \Rightarrow {A_1} = 20\,\,\left( {cm} \right)\) Tại thời điểm \(t = \dfrac{\pi }{{10}}\,\,s\), khoảng cách giữa hai vật là: \(d = \sqrt {{{60}^2} + {{70}^2}} = 92,2\,\,\left( {cm} \right)\) Chọn D. Câu hỏi 13 : Một lò xo nhẹ có độ cứng \(20 N/m,\) đặt trên mặt phẳng ngang rất dài, một đầu cố định vào bức tường thẳng đứng, đầu còn lại gắn vật nặng \(m_1= 80g.\) Vật \(m_2 = 200g,\) mang điện tích \(20\;\mu C\) được liên kết với \(m_1\) bằng một sợi dây cách điện không dãn dài \(20cm.\) Hệ thống được đặt trong điện trường đều nằm ngang, theo hướng xa điểm cố định của lò xo và có cường độ \(20000 V/m.\) Bỏ qua ma sát giữa \(m_1\) với mặt phẳng ngang, hệ số ma sát giữa \(m_2\) và mặt phẳng ngang là \(0,1.\) Lấy \({\pi ^2} = 10\) và \(g = 10m/s^2.\) Tại thời điểm \(t = 0\) đốt sợi dây nối hai vật thì \(m_1\) dao động điều hòa, đến thời điểm \(t = 1,25s\) thì khoảng cách giữa hai vật gần giá trị nào nhất sau đây?
Đáp án: A Phương pháp giải: Khi đốt sợi dây thì vật \(m_1\) dao động điều hòa với biên độ \(A,\) chu kì \(T_1\) còn vật \(m_2\) chuyển động nhanh dần đều với gia tốc \(a_2.\) Công thức tính độ lớn lực điện: \({F_d} = \left| q \right|E\) Sử dụng định luật II Niuton tính gia tốc \(a_2.\) Công thức tính quãng đường của chuyển động thẳng biến đổi đều: \(s = \dfrac{1}{2}a{t^2}\) Lời giải chi tiết: Khi đốt sợi dây thì vật \(m_1\) dao động điều hòa với biên độ \(A,\) chu kì \(T_1\) còn vật \(m_2\) chuyển động nhanh dần đều với gia tốc \(a_2.\) Công thức tính độ lớn lực điện: \({F_d} = \left| q \right|E\) Ta có: \(\left\{ \begin{array}{l}A = \dfrac{{{F_d}}}{k} = \dfrac{{\left| q \right|E}}{k}\\{T_1} = 2\pi \sqrt {\dfrac{{{m_1}}}{k}} \\{a_2} = \dfrac{{{F_d} - {F_{mst}}}}{{{m_2}}} = \dfrac{{\left| q \right|E - \mu {m_2}g}}{{{m_2}}}\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}A = \dfrac{{{{20.10}^{ - 6}}.20000}}{{20}} = 0,02m\\{T_1} = 2\pi .\sqrt {\dfrac{{0,08}}{{20}}} = 0,4s\\{a_2} = \dfrac{{{{20.10}^{ - 6}}.20000 - 0,1.0,2.10}}{{0,2}} = 1m/{s^2}\end{array} \right.\) Tại thời điểm \(t = 1,25s = 3T + \dfrac{T}{8}\) + Vật \(m_1\) có li độ: \({x_1} = \dfrac{A}{{\sqrt 2 }}\) + Vật \(m_2\) đi được quãng đường: \({s_2} = \dfrac{1}{2}{a_2}{t^2} = \dfrac{1}{2}.1.1,{25^2} = 0,78125m\) Khoảng cách giữa hai vật là: \(d = A - \dfrac{A}{{\sqrt 2 }} + l + {s_2}\) \( \Rightarrow d = 0,02 - \dfrac{{0,02}}{{\sqrt 2 }} + 0,2 + 0,78125 = 0,987m = 98,7cm\) Chọn A. Câu hỏi 14 : Một con lắc lò xo treo thẳng đứng gồm quả cầu nhỏ có khối lượng m = 150g và lò xo có độ cứng k = 60 N/m. Người ta đưa quả cầu đến vị trí lò xo không bị biến dạng rồi truyền cho nó một vận tốc ban đầu \({v_0} = \frac{{\sqrt 3 }}{2}m/s\) theo phương thẳng đứng hướng xuống. Sau khi được truyền vận tốc con lắc dao động điều hòa. Chọn thời điểm t = 0 là lúc quả cầu được truyền vận tốc, lấy m/s2. Thời gian ngắn nhất tính từ lúc t = 0 đến lúc lực đàn hồi tác dụng lên vật có độ lớn 3 N là
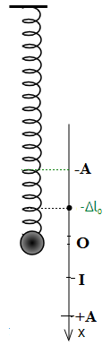
Đáp án: B Phương pháp giải: Tại vị trí cân bằng, lò xo dãn là \(\Delta l = \frac{{mg}}{k}\) Biểu thức tính tần số góc \(\omega = \sqrt {\frac{k}{m}} \) Áp dụng công thức độc lập với thời gian \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\) Biểu thức độ lớn lực đàn hồi \(F = k\Delta l\) Lời giải chi tiết: Tại vị trí cân bằng, lò xo dãn: \(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,15.10}}{{60}} = 0,025m = 2,5cm\) Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = 20rad/s\) Biên độ dao động: \(\begin{array}{l} Tại t = 0 tức là lúc truyền vận tốc thì lò xo không giãn: Fđh = 0N. Khi lực đàn hồi là 3N thì: \(F = k\Delta l \Rightarrow \Delta l = \frac{3}{{60}} = 0,05m = 5cm\) Ta có hình vẽ:
I là vị trí mà lò xo dãn 5cm, x = 2,5cm Thời gian t là: \(t = \frac{{ar\sin \frac{{2,5}}{5} + ar\sin \frac{{2,5}}{5}}}{{2\pi }}.T = \frac{T}{6} = \frac{{2\pi }}{{\omega .6}} = \frac{{2\pi }}{{20.6}} = \frac{\pi }{{60}}s\) Chọn B. Câu hỏi 15 : Một con lắc lò xo treo thẳng đứng, dao động điều hòa với biên độ A, chu kì T. Khi vật ở vị trí cân bằng, tại nơi có gia tốc trọng trường g, lò xo giãn một đoạn l = 0,5A. Thời gian trong một chu kì mà độ lớn gia tốc của vật đó lớn hơn hoặc bằng gia tốc trọng trường g là
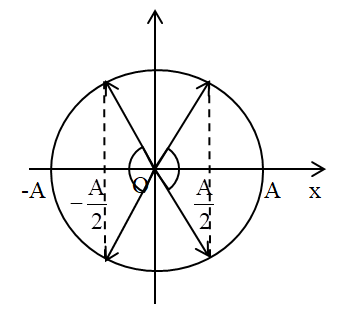
Đáp án: D Phương pháp giải: Độ lớn gia tốc của vật dao động: \(a = {\omega ^2}x = \dfrac{g}{{\Delta {\rm{l}}}}x\) Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \dfrac{{\Delta \varphi .T}}{{2\pi }}\) Lời giải chi tiết: Độ lớn gia tốc của vật là: \(a = \left| {\dfrac{g}{{\Delta {\rm{l}}}}x} \right| = \dfrac{g}{{0,5A}}\left| x \right| = \dfrac{{2g\left| x \right|}}{A}\)Độ lớn gia tốc của vật đó lớn hơn hoặc bằng gia tốc trọng trường g, ta có: \(a \ge g \Rightarrow \dfrac{{2g\left| x \right|}}{A} \ge g \Rightarrow \left| x \right| \ge \dfrac{A}{2} \Rightarrow \left\{ \begin{array}{l}x \ge \dfrac{A}{2}\\x \le - \dfrac{A}{2}\end{array} \right.\) Ta có vòng tròn lượng giác: Từ vòng tròn lượng giác, ta thấy trong 1 chu kì, vật có độ lớn gia tốc lớn hơn hoặc bằng gia tốc trọng trường khi vecto quay được góc: \(\Delta \varphi = 2.\dfrac{{2\pi }}{3} = \dfrac{{4\pi }}{3}\,\,\left( {rad} \right)\) Thời gian vật có độ lớn gia tốc lớn hơn hoặc bằng gia tốc trọng trường trong 1 chu kì là: \(\Delta t = \dfrac{{\Delta \varphi .T}}{{2\pi }} = \dfrac{{\dfrac{{4\pi }}{3}.T}}{{2\pi }} = \dfrac{{2T}}{3}\) Chọn D. Câu hỏi 16 : Một con lắc được treo vào một điểm cố định, đang dao động điều hòa theo phương thẳng đứng. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của độ lớn của lực kéo về và độ lớn của lực đàn hồi của lò xo tác dụng lên vật theo thời gian. Lấy g = 10 m/s2. Biết \({t_2} - {t_1} = \frac{{7\pi }}{{120}}s\). Tốc độ cực đại của con lắc gần nhất với giá trị nào sau đây?
Đáp án: B Phương pháp giải: Biểu thức lực hồi phục: \(F = - kx\) Biểu thức lực đàn hồi: \(F = - k\left( {x + \Delta {l_0}} \right)\) Từ đồ thị dễ thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục. Đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị, ta tìm được ∆l0 theo A Thời điểm t1 ứng với vị trí lò xo không dãn. Thời điểm t2 ứng với vị trí cân bằng. Sử dụng ĐTLG từ thời điểm t1 đến t2 tìm được chu kì T, ∆l0 và A. Tốc độ cực đại: \({v_{\max }} = \omega A = A.\sqrt {\frac{g}{{\Delta l}}} \) Lời giải chi tiết: Biểu thức lực hồi phục và lực đàn hồi: \(\left\{ \begin{array}{l} Từ đồ thị dễ thấy đường có đỉnh đạt 4 đơn vị là biểu diễn lực hồi phục. Đường có đỉnh đạt 6 đơn vị là biểu diễn lực đàn hồi. Lập tỉ số tại các cực trị: \(\frac{{{F_{dh\max }}}}{{{F_{hp\max }}}} = \frac{{k.(A + \Delta {l_0})}}{{kA}} = \frac{6}{4} \Rightarrow \Delta {l_0} = \frac{A}{2}\) Thời điểm t1 ứng với vị trí lò xo không dãn. Thời điểm t2 ứng với vị trí cân bằng. Sử dụng ĐTLG từ thời điểm t1 đến t2 Thời gian từ t1 đến t2 là : \(\begin{array}{l} Với \(\omega = \sqrt {\frac{g}{{\Delta {l_0}}}} \Rightarrow 20 = \sqrt {\frac{{10}}{{\Delta {l_0}}}} \Rightarrow \Delta {l_0} = 0,025m = 2,5cm \Rightarrow A = 5cm\) Tốc độ cực đại: \(v = \omega A = 20.5 = 100\left( {cm/s} \right)\) Gần nhất với giá trị 98 cm/s Chọn B.
Câu hỏi 17 : Hai vật A và B có cùng khối lượng 1 kg và có kích thước nhỏ được nối với nhau bởi sợi dây mảnh nhẹ dài 20 cm, hai vật được treo vào một lò xo có độ cứng 100 N/m tại nơi có gia tốc trọng trường g = 10 m/s2. Cho π2 = 10. Khi hệ vật và lò xo đang ở vị trí cân bằng, người ta đốt sợi dây nối hai vật và vật B sẽ rơi tự do còn vật A sẽ dao động điều hòa. Lần đầu tiên vật A lên đến vị trí cao nhất thì khoảng cách giữa hai vật bằng
Đáp án: B Phương pháp giải: Áp dụng công thức tính độ dãn ban đầu của lò xo là \(\Delta {l_0} = \frac{{2mg}}{k}\) Khi đốt sợi dây thì độ dãn của lò xo là \(\Delta {l_1} = \frac{{mg}}{k}\) Sau khi đốt sợi dây, vật A gắn với lò xo dao động điều hòa với biên độ \(A = \Delta {l_0} - \Delta {l_1}\) và chu kì \(T = 2\pi \sqrt {\frac{m}{k}} \) Thời gian để vật A đến vị trí cao nhất là nửa chu kì, vì ban đầu nó ở vị trí thấp nhất. Vật B rơi tự do, quãng đường vật B đi được trong khoảng thời gian t là \(S = \frac{1}{2}.g.{t^2}\) Khoảng cách giữa vật A và B khi đó là \(L = 2A + l + {S_B}\) Lời giải chi tiết: Độ dãn ban đầu của lò xo: \(\Delta {l_0} = \frac{{2mg}}{k} = \frac{{2.10}}{{100}} = 0,2m = 20cm\) Khi đốt sợi dây thì độ dãn của lò xo là \(\Delta {l_1} = \frac{{mg}}{k} = \frac{{1.10}}{{100}} = 0,1m = 10cm\) Sau khi đốt sợi dây, vật A gắn với lò xo sẽ dao động điều hòa với biên độ và chu kì: \(\left\{ \begin{array}{l} Thời gian để vật A đến vị trí cao nhất là nửa chu kì, vì ban đầu nó ở vị trí thấp nhất, nên \(t = \frac{T}{2} = \frac{1}{\pi }s\) Vật B rơi tự do, quãng đường vật B đi được trong khoảng thời gian t là: \(S = \frac{1}{2}.g.{t^2} = \frac{1}{2}.10.{\left( {\frac{1}{\pi }} \right)^2} = 0,5m = 50cm\) Khoảng cách giữa vật A và B khi đó là: \(L = 2A + l + {S_B} = 2.10 + 20 + 50 = {90_{}}cm\) Chọn B. Câu hỏi 18 : Một lò xo nhẹ cách điện có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\) một đầu cố định, đầu còn lại gắn vào quả cầu nhỏ tích điện \(q = + 5\mu C\), khối lượng \(m{\rm{ }} = {\rm{ }}200g\). Quả cầu có thể dao động không ma sát dọc theo trục lò xo nằm ngang và cách điện. Tại thời điểm ban đầu t = 0 kéo vật tới vị trí lò xo giãn 4 cm rồi thả nhẹ đến thời điểm t = 0,2 s thì thiết lập điện trường không đổi trong thời gian 0,2 s, biết điện trường nằm ngang dọc theo trục lò xo hướng ra xa điểm cố định và có độ lớn \(E{\rm{ }} = {\rm{ }}{10^5}V/m\) . Lấy \(g{\rm{ }} = {\rm{ }}10m/{s^2}\). trong quá trình dao động thì tốc độ cực đại mà quả cầu đạt được là
Đáp án: D Phương pháp giải: + Sử dụng biểu thức: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 0,4s\) + Xác định lực điện + Sử dụng biểu thức tính tốc độ cực đại: \({v_{max}} = \omega A\) Lời giải chi tiết: Ta có: + Chu kì dao động: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 0,4s\) + Biên độ dao động ban đầu: \({A_0} = 4cm\) + Tại thời điểm \(t = 0\): \(x = 4cm\) + Tại thời điểm \(t = 0,2s = \dfrac{T}{2}\): \(x' = 4cm\) và khi đó thiết lập điện trường không đổi trong thời gian \(0,2s\) Vì \(\overrightarrow E \) hướng ra xa điểm cố định và điện tích \(q > 0\) nên \(\overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow E \) \( \Rightarrow \) Vị trí cân bằng khi có điện trường lệch ra xa điểm cố định \({x_0} = \dfrac{{qE}}{m} = 0,01m = 1cm\) \( \Rightarrow \) Biên độ khi có điện trường: \({A_1} = {A_0} + {x_0} = 4 + 1 = 5cm\)Điện trường không còn sau \(0,2s = \dfrac{T}{2}\) vật sẽ dao động điều hòa quanh vị trí cân bằng ban đầu \( \Rightarrow \) Biên độ trong giai đoạn này: \({A_2} = {A_1} + {x_0} = 6cm\) \( \Rightarrow \) Tốc độ cực đại: \({v_{max}} = \omega {A_2} = \dfrac{{2\pi }}{{0,4}}.6 = 30\pi \left( {cm/s} \right)\) Chọn D Câu hỏi 19 : Một con lắc lò xo đang dao động điều hòa với biên độ \(5\,\,cm\) và chu kì \(0,5\,\,s\) trên mặt phẳng nằm ngang. Khi vật nhỏ của con lắc có tốc độ \(v\) thì người ta giữ chặt một điểm trên lò xo, vật tiếp tục dao động điều hòa với biên độ \(2,25\,\,cm\) và chu kì \(0,25\,\,s\). Giá trị của \(v\) gần nhất với giá trị nào sau đây?
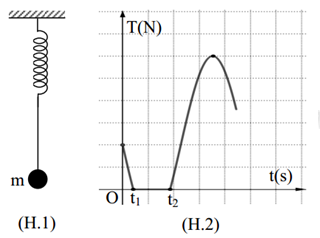
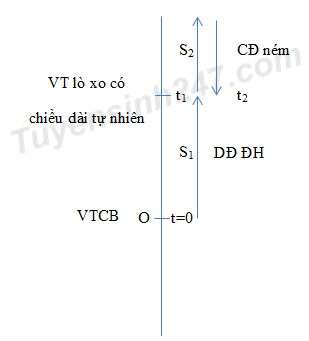
Đáp án: A Phương pháp giải: Chu kì của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \) Tốc độ góc của con lắc: \(\omega = \dfrac{{2\pi }}{T}\) Giữ lò xo: \(k'x' = kx\) Tốc độc của vật dao động: \(v = \omega \sqrt {{A^2} - {x^2}} = \sqrt {\dfrac{k}{m}} .\sqrt {{A^2} - {x^2}} \) Lời giải chi tiết: Chu kì của con lắc trước và sau khi giữ lò xo: \(\left\{ \begin{array}{l}T = 2\pi \sqrt {\dfrac{m}{k}} \\T' = 2\pi \sqrt {\dfrac{m}{{k'}}} \end{array} \right. \Rightarrow {\left( {\dfrac{T}{{T'}}} \right)^2} = \dfrac{{k'}}{k} \Rightarrow \dfrac{{k'}}{k} = {\left( {\dfrac{{0,5}}{{0,25}}} \right)^2} = 4\) Trước khi giữ lò xo, vật có li độ \(x\), sau khi giữ lò xo, vật có li độ \(x'\): \(k'x' = kx \Rightarrow x' = \dfrac{k}{{k'}}x = \dfrac{x}{4}\) Tốc độ của vật trước và sau khi giữ lò xo không đổi: \(\begin{array}{l}v = \sqrt {\dfrac{k}{m}} .\sqrt {{A^2} - {x^2}} = \sqrt {\dfrac{{k'}}{m}} .\sqrt {A{'^2} - x{'^2}} \\ \Rightarrow k.\left( {{A^2} - {x^2}} \right) = k'.\left( {A{'^2} - x{'^2}} \right)\\ \Rightarrow k.\left( {{5^2} - {x^2}} \right) = 4k.\left[ {2,{{25}^2} - {{\left( {\dfrac{x}{4}} \right)}^2}} \right] \Rightarrow x = \sqrt {\dfrac{{19}}{3}} \,\,\left( {c{m^2}} \right)\\ \Rightarrow v = \omega \sqrt {{A^2} - {x^2}} = \dfrac{{2\pi }}{T}.\sqrt {{A^2} - {x^2}} = \dfrac{{2\pi }}{{0,5}}.\sqrt {{5^2} - {{\left( {\sqrt {\dfrac{{19}}{3}} } \right)}^2}} \approx 54,29\,\,\left( {cm/s} \right)\end{array}\) Chọn A. Câu hỏi 20 : Lò xo nhẹ một đầu cố định, đầu còn lại gắn vào sợi dây mềm, không dãn có treo vật nhỏ m như hình vẽ (H.1). Khối lượng dây và sức cản của không khí không đáng kể. Tại \(t = 0\), m đang đứng yên ở vị trí cân bằng thì được truyền vận tốc \({v_0}\) thẳng đứng từ dưới lên. Sau đó lực căng dây T tác dụng vào m phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ (H.2). Biết lúc vật cân bằng lò xo giãn \(10cm\) và trong quá trình chuyển động m không va chạm với lò xo. Quãng đường m đi được kể từ lúc bắt đầu chuyển động đến thời điểm \({t_2}\) bằng
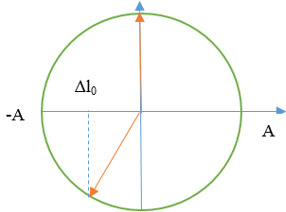
Đáp án: B Phương pháp giải: + Vận dụng lí thuyết về lực căng dây và lực đàn hồi + Sử dụng công thức tính lực đàn hồi: \({F_{dh}} = k.\left( {\Delta l + x} \right)\) + Đọc đồ thị \(T - t\) Lời giải chi tiết: Ta có: \(\Delta {l_0} = 10cm\) Lực căng dây \(T = {F_{dh}}\) \( \Rightarrow \) \({T_{max}}\) khi \({F_{d{h_{max}}}}\) Tại thời điểm ban đầu: \(t = 0\) thì \(T = \dfrac{2}{6}{T_{max}}\) lực đàn hồi khi này \({F_{d{h_0}}} = k.\Delta {l_0} = \dfrac{1}{3}{T_{max}}\) \(\begin{array}{l} \Rightarrow \dfrac{{{F_{d{h_0}}}}}{{{F_{d{h_{max}}}}}} = \dfrac{{\dfrac{1}{3}{T_{max}}}}{{{T_{max}}}} = \dfrac{1}{3} = \dfrac{{k\Delta {l_0}}}{{k\left( {\Delta {l_0} + A} \right)}}\\ \Rightarrow A = 2\Delta {l_0} = 20cm\end{array}\) Dây trùng khi lò xo nén và dây căng khi lò xo dãn Ta có: \({S_1} = 10cm\) \({S_2} = {h_{max}}\) ta có \(\dfrac{1}{2}m{v^2} = mg{h_{max}}\) \( \Rightarrow {S_2} = \dfrac{{{v^2}}}{{2g}}\) Lại có vị trí ném có li độ \(x = - \Delta {l_0} = - \dfrac{A}{2}\) suy ra vận tốc tại đó: \(v = - \omega A\dfrac{{\sqrt 3 }}{2}\) \( \Rightarrow {S_2} = \dfrac{{3{A^2}}}{{8\Delta {l_0}}} = \dfrac{{{{3.20}^2}}}{{8.10}} = 15cm\) \( \Rightarrow \) Quãng đường vật m đi được từ thời điểm ban đầu đến \({t_2}\) là: \(S = {S_1} + 2{S_2} = 10 + 2.15 = 40cm\) Chọn B Câu hỏi 21 : Một lò xo nhẹ làm bằng vật liệu cách điện có độ cứng k = 50N/m, một đầu được gắn cố định, đầu còn lại gắn vào quả cầu nhỏ tích điện q = 5µC, khối lượng m = 50g. Quả cầu có thể dao động không ma sát dọc theo trục lò xo nằm ngang và cách điện. Tại thời điểm ban đầu t = 0 kéo vật tới vị trí lò xo dãn 4 cm rồi thả nhẹ đến thời điểm t = 0,1 s thì thiết lập điện trường không đổi trong thời gian 0,1 s, biết điện trường nằm ngang dọc theo trục lò xo hướng ra xa điểm cố định và có độ lớn E = 105 V/m. Lấy g = 10 m/s2, π2 = 10 . Trong quá trình dao động thì tốc độ cực đại mà quả cầu đạt được gần nhất giá trị nào sau đây?
Đáp án: B Phương pháp giải: + Xác định tần số góc, và chu kì dao động ban đầu của hệ dao động. Xác định vị trí của vật mà ta thiết lập điện trường \(\overrightarrow E \). + Khi đó, vật chịu tác dụng của lực điện, vì q > 0 nên lực điện cùng chiều \(\overrightarrow E \). Vị trí cân bằng của vật lúc này thay đổi một đoạn ∆l0với \(F = q.E = k.\Delta {l_0}\) Do đó vật dao động với biên độ mới. Áp dụng công thức xác định tần số góc và chu kì: \(\omega = \sqrt {\frac{k}{m}} ;T = \frac{{2\pi }}{\omega }\) Vận tốc cực đại mới là: \({v_{\max }}' = \omega .A'\) Lời giải chi tiết: Ta có hình vẽ:
Tần số góc và chu kì: \(\left\{ \begin{array}{l} Ban đầu kéo vật khỏi vị trí cân bằng 4cm, rồi thả nhẹ thì vật dao động với biên độ A = 4cm, chu kì T = 0,2s. Sau khi chuyển động được 0,1s vật đi đến vị trí biên âm. Ta thiết lập điện trường E thì vật chịu tác dụng của lực điện trường \(\overrightarrow F = q.\overrightarrow E \) do đó vị trí cân bằng bị thay đổi ∆l0 với: \(F = q.E = k.\Delta {l_0} \Rightarrow \Delta {l_0} = \frac{{{{5.10}^{ - 6}}{{.10}^5}}}{{50}} = 0,01m = 1cm\) Biên độ dao động mới: \(A' = A + \Delta {l_0}\; = 4 + 1 = 5cm\) Vận tốc cực đại mới là: \({v_{\max }}' = \omega .A' = 10\pi .5 \approx 158,5cm/s\) Vậy giá trị gần nhất là 160 cm/s Chọn B.
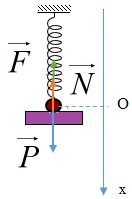
Câu hỏi 22 : Một lò xo nhẹ có độ cứng 100N/m, đầu trên gắn cố định, đầu dưới treo quả cầu nhỏ có khối lượng m = 1kg sao cho vật có thể dao động không ma sát theo phương thẳng đứng trùng với trục của lò xo. Lúc đầu dùng giá nằm ngang đỡ m để lò xo không biến dạng. Sau đó cho giá đỡ chuyển động thẳng đứng xuống dưới nhanh dần đều với gia tốc 2m/s2. Bỏ qua mọi ma sát. Lấy gia tốc trọng trường g = 10m/s2. Khi m rời khỏi giá đỡ nó dao động điều hòa. Biên độ dao động điều hòa là
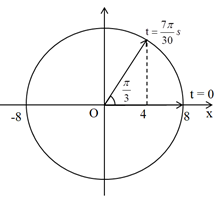
Đáp án: C Phương pháp giải: Vẽ hình biểu diễn các lực tác dụng vào vật nặng khi vật năng di chuyển. Áp dụng định luật II Niu- tơn: \(\overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a \) Khi vật rời khỏi tấm ván đỡ thì phản lực \(\overrightarrow N \) = 0. Ta tìm được vị trí vật rời khỏi giá đỡ thì lò xo giãn ∆l, khi đó Vị trí cân bằng là vị trí lò xo giãn ∆l0thỏa mãn: \(\Delta {l_0} = \frac{{mg}}{k}\) Lời giải chi tiết: Ta có hình vẽ: Áp dụng định luật II Niu- tơn: \(\overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a \) Khi vật rời khỏi tấm ván đỡ thì phản lực \(\overrightarrow N \) = 0. Ta có : \(\overrightarrow F + \overrightarrow P = m\overrightarrow a \) Chiếu lên Ox ta được: \(\begin{array}{l} Vị trí cân bằng là vị trí lò xo giãn ∆l0 thỏa mãn: \(\Delta {l_0} = \frac{{mg}}{k} = \frac{{1.10}}{{100}} = 0,1m = 10cm\) Vậy li độ của dao động là: \(x = 8-10 = - 2cm\) Vận tốc của vật khi đó là \(v = \sqrt {2as} = \sqrt {2.2.8} = \sqrt {32} cm/s\) Vậy biên độ dao động của vật là \(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = 6cm\) Chọn C. Câu hỏi 23 : Một con lắc lò xo được đặt nằm ngang gồm lò xo có độ cứng \(k = 40\,\,N/m\) và vật nặng khối lượng \(m = 400\,\,g\). Từ vị trí cân bằng kéo vật ra một đoạn \(8\,\,cm\) rồi thả nhẹ cho vật dao động điều hòa. Sau khi thả vật \(\dfrac{{7\pi }}{{30}}\,\,s\) thì giữ đột ngột điểm chính giữa của lò xo khi đó. Biên độ dao động của vật sau khi giữ lò xo là
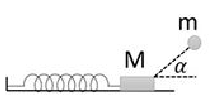
Đáp án: C Phương pháp giải: Tần số góc của con lắc: \(\omega = \sqrt {\dfrac{k}{m}} \) Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi = \omega .\Delta t\) Giữ lò xo: \(k'x' = kx\) Công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2}\) Lời giải chi tiết: Tần số góc của con lắc là: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{40}}{{0,4}}} = 10\,\,\left( {rad/s} \right)\) Trong thời gian \(\dfrac{{7\pi }}{{30}}\,\,s\), vecto quay được góc: \(\Delta \varphi = \omega .\Delta t = 10.\dfrac{{7\pi }}{{30}} = \dfrac{{7\pi }}{3} = 2\pi + \dfrac{\pi }{3}\,\,\left( {rad} \right)\) Ta có vòng trong lượng giác: Từ vòng tròn lượng giác ta thấy tại thời điểm \(\dfrac{{7\pi }}{{30}}\,\,s\), vật có li độ \(x = 4\,\,cm\) Áp dụng công thức độc lập với thời gian ta có: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow v = \omega .\sqrt {{A^2} - {x^2}} = 10.\sqrt {{8^2} - {4^2}} = 40\sqrt 3 \,\,\left( {cm/s} \right)\) Giữ điểm chính giữa lò xo, li độ mới của vật tại điểm giữ là: \(x' = \dfrac{x}{2} = 2\,\,\left( {cm} \right)\) Độ cứng của lò xo khi đó: \(k'x' = kx \Rightarrow k' = \dfrac{{kx}}{{x'}} = 2k = 80\,\,\left( {N/m} \right)\) Tần số góc của con lắc mới là: \(\omega ' = \sqrt {\dfrac{{k'}}{m}} = \sqrt {\dfrac{{80}}{{0,4}}} = 10\sqrt 2 \,\,\left( {rad/s} \right)\) Giữ lò xo, vận tốc của vật không thay đổi. Áp dụng công thức độc lập với thời gian, ta có: \(x{'^2} + \dfrac{{{v^2}}}{{\omega {'^2}}} = A{'^2} \Rightarrow {2^2} + \dfrac{{{{\left( {40\sqrt 3 } \right)}^2}}}{{{{\left( {10\sqrt 2 } \right)}^2}}} = A{'^2} \Rightarrow A' = 2\sqrt 7 \,\,\left( {cm} \right)\) Chọn C. Câu hỏi 24 : Một con lắc lò xo nằm ngang gồm lò xo có khối lượng không đáng kể, độ cứng k = 100 N/m gắn với vật có khối lượng M = 400 g. Khi M đang đứng yên tại vị trí lò xo không biến dạng thì vật m bay từ phía trên tới va chạm và dính vào M. Biết rằng va chạm giữa m và M là va chạm mềm; hệ số ma sát trượt giữa hệ vật (m + M) và mặt nằm ngang là 0,1; khối lượng m = 100 g; khi m tiếp xúc với M, vận tốc của vật m là 20 m/s và hợp với phương ngang một góc 600; lấy g = 10 m/s2. Sau va chạm, độ giãn cực đại của lò xo gần nhất với giá trị nào sau đây?
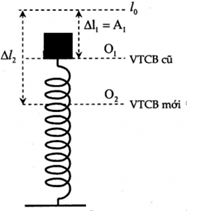
Đáp án: C Phương pháp giải: + Áp dụng định luật bảo toàn động lượng theo phương ngang cho hai vật m và M khi va chạm : \(m.v.\cos \alpha = (m + M).v'\) + Sau va chạm, hệ vật (m+M) dao động tắt dần do có ma sát, vị trí bị nén cực đại cách vị trí cân bằng A1. Áp dụng định luật bảo toàn năng lượng ta có: \(\frac{1}{2}.(m + M).v{'^2} = {F_{ms}}.{A_1} + \frac{1}{2}.k.A_1^2 = \mu .(m + M).g.{A_1} + \frac{1}{2}.k.A_1^2\) Tìm được A1 + Sau đó vật chuyển động sang trái, khi đó lò xo bị giãn đến vị trí cách vị trí cân bằng A2 Ta có: \(\frac{1}{2}.k.A_1^2 - \frac{1}{2}.k.A_2^2 = \mu .(m + M).g.({A_1} + {A_2})\) Tìm được A2 chính là độ giãn cực đại của lò xo. Lời giải chi tiết: Áp dụng định luật bảo toàn động lượng theo phương ngang cho hai vật m và M khi va chạm. \(\begin{array}{l} Sau va chạm, hệ vật (m+M) dao động tắt dần do có ma sát, vị trí bị nén cực đại cách vị trí cân bằng A1. Áp dụng định luật bảo toàn năng lượng ta có: \(\begin{array}{l} Sau đó vật chuyển động sang trái, khi đó lò xo bị giãn đến vị trí cách vị trí cân bằng A2 Ta có: \(\begin{array}{l} Tìm được A2 = 12,65cm chính là độ giãn cực đại của lò xo. Chọn C. Câu hỏi 25 : Một con lắc lò xo treo thẳng đứng, lò xo có độ cứng k = 100 N/m, vật nặng có khối lượng m = 0,2 kg. Ban đầu đưa vật đến vị trí lò xo không biến dạng rồi thả nhẹ. Khi vật đi qua vị trí cân bằng, người ta chồng nhẹ một vật cùng khối lượng lên vật m, lấy \(g = 10\,\,m/{s^2}\). Biên độ dao động của hệ hai vật sau đó là
Đáp án: C Phương pháp giải: Khi ở vị trí cân bằng, lò xo nén một đoạn: \(\Delta l = \dfrac{{mg}}{k}\) Vận tốc của hệ sau va chạm: \(v' = \dfrac{{mv}}{{m + m'}}\) Công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2}\) Lời giải chi tiết: Gọi O1, O2 là vị trí cân bằng trước và sau khi đặt thêm vật, chiều dương hướng lên. + Trước khi đặt thêm vật: Ban đầu đưa vật đến vị trí lò xo không biến dạng rồi buông nhẹ, biên độ dao động khi đó là: \({A_1} = \Delta {l_1} = \dfrac{{mg}}{k} = \dfrac{{0,2.10}}{{100}} = 0,02\,\,\left( m \right) = 2\,\,\left( {cm} \right)\) Tần số góc của con lắc là: \({\omega _1} = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{100}}{{0,2}}} = 10\sqrt 5 \,\,\left( {rad/s} \right)\) Vận tốc của vật ở vị trí cân bằng là: \({v_{\max 1}} = {A_1}{\omega _1} = 2.10\sqrt 5 = 20\sqrt 5 \,\,\left( {cm/s} \right)\) + Sau khi đặt thêm vật: Vận tốc của hệ là: \(v = \dfrac{{m{v_{\max 1}}}}{{m + m}} = \dfrac{{0,2.20\sqrt 5 }}{{0,2 + 0,2}} = 10\sqrt 5 \,\,\left( {cm/s} \right)\) Vị trí cân bằng mới của hệ dịch xuống một đoạn: \({O_1}{O_2} = \Delta {l_2} - \Delta {l_1} = \dfrac{{2mg}}{k} - \dfrac{{mg}}{k} = \dfrac{{mg}}{k} = \dfrac{{0,2.10}}{{100}} = 0,02\,\,\left( m \right) = 2\,\,\left( {cm} \right)\) Li độ của vật lúc này là: \(x = {O_1}{O_2} = 2\,\,\left( {cm} \right)\) Tần số góc của hệ là: \(\omega = \sqrt {\dfrac{k}{{m + m}}} = \sqrt {\dfrac{{100}}{{0,2 + 0,2}}} = 5\sqrt {10} \,\,\left( {rad/s} \right)\) Biên độ của hệ dao động là: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {2^2} + \dfrac{{{{\left( {10\sqrt 5 } \right)}^2}}}{{{{\left( {5\sqrt {10} } \right)}^2}}} = {A^2} \Rightarrow A = \sqrt 6 \,\,\left( {cm} \right)\) Chọn C. Câu hỏi 26 : Một vật nhỏ khối lượng M = 0,6 kg gắn trên một lò xo nhẹ thẳng đứng có độ cứng 200 N/m, đầu dưới của lò xo gắn cố định. Một vật nhỏ có khối lượng m = 0,3 kg rơi tự do từ độ cao h = 0,6 m xuống va chạm mềm với M. Sau va chạm hai vật dính vào nhau và cùng dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Lấy gia tốc trọng trường \(g = 10\,\,m/{s^2}\). Biên độ của dao động là
Đáp án: D Phương pháp giải: Vận tốc của vật rơi tự do: \({v_0} = \sqrt {2gh} \) Vận tốc của hệ sau va chạm: \(v = \dfrac{{m{v_0}}}{{m + M}}\) Tần số góc của hệ: \(\omega = \sqrt {\dfrac{k}{{m + M}}} \) Độ dịch chuyển vị trí cân bằng: \(x = \dfrac{{mg}}{k}\) Công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2}\) Lời giải chi tiết: Tần số góc của hệ sau va chạm là: \(\omega = \sqrt {\dfrac{k}{{m + M}}} = \sqrt {\dfrac{{200}}{{0,3 + 0,6}}} = \dfrac{{20\sqrt 5 }}{3}\,\,\left( {rad/s} \right)\) Vận tốc của hệ sau va chạm là: \(v = \dfrac{{m{v_0}}}{{m + M}} = \dfrac{{m\sqrt {2gh} }}{{m + M}} = \dfrac{{0,3.\sqrt {2.10.0,6} }}{{0,3 + 0,6}} = \dfrac{{2\sqrt 3 }}{3}\,\,\left( {m/s} \right) = \dfrac{{200}}{{\sqrt 3 }}\,\,\left( {cm/s} \right)\) Độ dịch chuyển vị trí cân bằng là: \(x = \dfrac{{mg}}{k} = \dfrac{{0,3.10}}{{200}} = 0,015\,\,\left( m \right) = 1,5\,\,\left( {cm} \right)\) Ta có công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow 1,{5^2} + \dfrac{{{{\left( {\dfrac{{200}}{{\sqrt 3 }}} \right)}^2}}}{{{{\left( {\dfrac{{20\sqrt 5 }}{3}} \right)}^2}}} = {A^2} \Rightarrow A = 7,9\,\,\left( {cm} \right)\) Chọn D. Câu hỏi 27 : Một con lắc lò xo có độ cứng 200 N/m, vật nặng có m = 0,4 kg dao động điều hòa trên mặt phẳng nằm ngang với biên độ \({\rm{3}}\sqrt 5 \,\,{\rm{cm}}\). Tại thời điểm vật m qua vị trí cân bằng thì một vật nhỏ có khối lượng m0 = 0,1 kg rơi thẳng đứng và dính vào m. Biên độ của hệ (m + m0) là
Đáp án: A Phương pháp giải: Tần số góc của hệ dao động: \(\omega = \sqrt {\dfrac{k}{m}} \) Vận tốc của vật khi qua vị trí cân bằng: \({v_{\max }} = A\omega \) Lời giải chi tiết: + Trước khi va chạm: Tần số góc của hệ dao động là: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{200}}{{0,4}}} = 10\sqrt 5 \,\,\left( {rad/s} \right)\) Vận tốc của vật khi ở vị trí cân bằng là: \({v_{\max }} = A\omega = 3\sqrt 5 .10\sqrt 5 = 150\,\,\left( {cm/s} \right)\) + Sau va chạm: Vận tốc của hệ là: \({v_{\max }}' = \dfrac{{m{v_{\max }}}}{{m + {m_0}}} = \dfrac{{0,4.150}}{{0,5}} = 120\,\,\left( {cm/s} \right)\) Tần số góc của hệ là: \(\omega ' = \sqrt {\dfrac{k}{{m + {m_0}}}} = \sqrt {\dfrac{{200}}{{0,4 + 0,1}}} = 20\,\,\left( {rad/s} \right)\) Biên độ dao động của hệ là: \(A' = \dfrac{{{v_{\max }}'}}{{\omega '}} = \dfrac{{120}}{{20}} = 6\,\,\left( {cm} \right)\) Chọn A. Câu hỏi 28 : Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng 50 N/m, vật nặng khối lượng M = 200 g có thể trượt không ma sát trên mặt phẳng ngang. Hệ đang ở trạng thái cân bằng, dùng vật m = 300 g bắn vào M theo phương nằm ngang với vận tốc 2 m/s. Sau khi va chạm, hai vật dính vào nhau và cùng dao động theo phương ngang trùng với trục của lò xo. Tính gia tốc cực đại của hệ (M + m)
Đáp án: C Phương pháp giải: Tần số góc của hệ sau va chạm: \(\omega = \sqrt {\dfrac{k}{{m + M}}} \) Vận tốc của hệ sau va chạm: \({v_1} = \dfrac{{mv}}{{M + m}}\) Biên độ dao động: \(A = \dfrac{{{v_{\max }}}}{\omega }\) Gia tốc cực đại: \({a_{\max }} = A{\omega ^2}\) Lời giải chi tiết: Tốc độ góc của hệ sau va chạm là: \(\omega = \sqrt {\dfrac{k}{{m + M}}} = \sqrt {\dfrac{{50}}{{0,2 + 0,3}}} = 10\,\,\left( {rad/s} \right)\) Vận tốc của hệ sau va chạm là: \({v_1} = \dfrac{{mv}}{{M + m}} = \dfrac{{0,3.2}}{{0,2 + 0,3}} = 1,2\,\,\left( {m/s} \right)\) Mà \({v_1} = {v_{\max }} \Rightarrow A = \dfrac{{{v_1}}}{\omega } = \dfrac{{1,2}}{{10}} = 0,12\,\,\left( m \right) = 12\,\,\left( {cm} \right)\) Gia tốc cực đại của hệ là: \({a_{\max }} = A{\omega ^2} = 0,{12.10^2} = 12\,\,\left( {m/{s^2}} \right)\) Chọn C. Câu hỏi 29 : Một con lắc lò xo treo thẳng đứng gồm vật nặng m = 100g, lò xo có độ cứng k = 40N/m. Từ vị trí cân bằng kéo vật xuống dưới 5cm rồi thả nhẹ cho nó dao động điều hòa. Lấy g = π2 = 10m/s2. Trong một chu kì, tốc độ trung bình của vật trong khoảng thời gian lò xo bị nén là
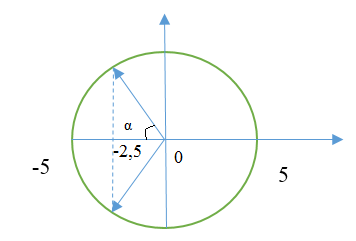
Đáp án: A Phương pháp giải: Khi vật ở vị trí cân bằng thì độ dãn của lò xo là \(\Delta {l_0} = \frac{{mg}}{k}\) Xác định biên độ dao động A = 5 cm, vị trí mà lò xo bị nén x0. Xác định thời gian lò xo bị nén trong một chu kì : \(t = 2.\frac{{\arccos \frac{{{x_0}}}{A}}}{\omega }\) và quãng đường vật đi được trong thời gian lò xo nén. Áp dụng công thức xác định vận tốc trung bình : \(v = \frac{S}{t}\) Lời giải chi tiết: Khi vật ở vị trí cân bằng thì độ dãn của lò xo là : \(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,1.10}}{{40}} = 0,{025_{}}m = 2,{5_{}}cm\) Vì kéo vật xuống khỏi vị trí cân bằng 5 cm rồi thả nhẹ nên biên độ : A = 5cm. Trong quá trình dao động, chọn chiều dương hướng xuống, gốc O ở vị trí cân bằng. Vậy lò xo bị nén khi chuyển động từ vị trí – 2,5cm đến – 5cm.
Vậy trong một chu kì, thời gian lò xo bị nén là: \(t = 2.\frac{\alpha }{\omega } = 2.\frac{{\arccos \frac{{2,5}}{5}}}{{\sqrt {\frac{k}{m}} }} = 2.\frac{{\frac{\pi }{3}}}{{\sqrt {\frac{{40}}{{0,1}}} }} = \frac{\pi }{{30}}s\) Quãng đường vật đi được là: S = 5cm. Vận tốc trung bình trong thời gian lò xo bị nén là: \(v = \frac{S}{t} = \frac{5}{{\frac{\pi }{{30}}}} = \frac{{150}}{\pi }\left( {cm/s} \right) = \frac{{1,5}}{\pi }\left( {m/s} \right)\) Chọn A.
Câu hỏi 30 : Một con lắc lò xo treo thẳng đứng đang dao động điều hòa. Hình bên là đồ thị mô tả sự phụ thuộc giữa độ lớn lực đàn hồi của lò xo theo thời gian t. Lấy g = π2 m/s2. Mốc thế năng tại vị trí cân bằng. Cơ năng của con lắc là:
Đáp án: D Phương pháp giải: Từ đồ thị ta thấy Fdhmax = 1,8N; Fmin = 0; sau đó Fdh tăng đến 0,6N rồi giảm; vậy lò xo có biên độ A lớn hơn độ dãn ∆l0 Áp dụng công thức lực đàn hồi \(F = k.\left( {x + \Delta {l_0}} \right)\) Vị trí khi t = 0 đến t = 0,1s thì F = 0, tức là vật ở vị trí lò xo không dãn. Ta sử dụng VTLG tìm chu kì, tần số góc. Áp dụng công thức tính năng lượng: \({\rm{W}} = \frac{1}{2}.k.{A^2}\) Lời giải chi tiết: + Từ đồ thị ta thấy Fdhmax = 1,8N; Fmin = 0; sau đó Fdh tăng đến 0,6 N rồi giảm; vậy lò xo có biên độ A lớn hơn độ dãn ∆l0 + Áp dụng công thức lực đàn hồi : \(\left\{ \begin{array}{l} \(\begin{array}{l} + Vị trí khi t = 0 thì F = 1,2N, vậy vật đang ở vị trí dãn một đoạn bằng A, tức là có tọa độ Đến t = 0,1s thì F = 0, tức là vật ở vị trí lò xo không dãn. + Ta có VTLG:
Vậy chu kì: \(T = 2.0,1 = 0,2s \Rightarrow \omega = \frac{{2\pi }}{T} = 10\pi \left( {rad/s} \right)\) Mà \(\omega = \sqrt {\frac{g}{{\Delta {l_0}}}} = 10\pi \Rightarrow \Delta {l_0} = 0,01m = 1cm\) Nên \(A = 2.\Delta {l_0} = 0,02m\) Ta có năng lượng của dao động là: \({\rm{W}} = \frac{1}{2}.k.{A^2} = \frac{1}{2}.k.A.A = \frac{1}{2}.1,2.0,02 = 0,012J = 12mJ\) Chọn D.
|













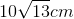
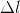 với: \(F = k\Delta \ell = 2N \Rightarrow \Delta \ell = 4cm\)
với: \(F = k\Delta \ell = 2N \Rightarrow \Delta \ell = 4cm\) 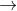 Biên độ dao động mới là A = 4cm
Biên độ dao động mới là A = 4cm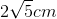
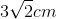
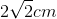



 cm
cm 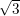 cm
cm