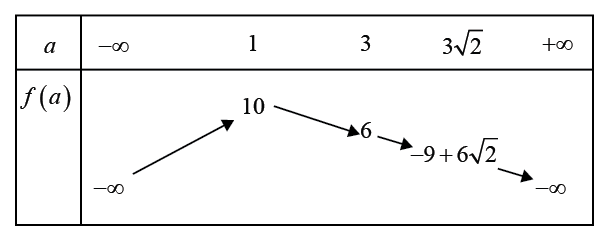
Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10

Đề bài

Câu 1 (3,0 điểm). Giải các bất phương trình sau:

1) ${x^2} + 3x - 1 + \left| {x + 1} \right| \le 0$

2) $\sqrt {4x + 1}  - \sqrt {3 - x}  \ge \sqrt {2x}$

Câu 2 (0.5 điểm).

Tìm tất cả các giá trị của m để bất phương trình sau: $\sqrt {3 + x}  + \sqrt {6 - x}  - \sqrt {(3 + x)(6 - x)}  \le m$ đúng $\forall x \in \left[ { - 3;6} \right].$

Câu 3 (3,0 điểm)

1) Cho $\cos \alpha  = \frac{1}{3};\alpha  \in \left( {\pi ;2\pi } \right)$ tính giá trị $\sin \alpha  =$? Và  $A = \frac{{1 - 4{{\sin }^2}x + {{\cos }^2}x}}{{3 + {{\sin }^2}x - 4\cos 2x}}.$

2) Chứng minh đẳng thức: $\frac{{1 + \sin 2x + \cos 2x}}{{1 + \sin 2x - \cos 2x}} = \cot x,$ với điều kiện biểu thức có nghĩa.

3) Chứng minh tam giác $ABC$ vuông nếu: $\frac{{\cos C}}{{\sin C - \cos A}} = \tan B.$

Câu 4 (2,5 điểm). Trong hệ tọa độ$Oxy,$ cho đường tròn $\left( C \right):\,\,{x^2} + {y^2} + 6x - 8y = 0$ và điểm $A\left( { - 1;4} \right)$ và đường thẳng $\Delta :2x - y + 1 = 0$

1) Xác định tọa độ tâm $I$ và bán kính của đường tròn $\left( C \right)$. Viết phương trình tiếp tuyến của đường tròn $\left( C \right)$ tại điểm $B\left( {0;8} \right).$

2) Viết phương trình đường tròn $\left( {C'} \right)$ có tâm $A\left( { - 1;\,\,4} \right)$ và cắt đường thẳng $\Delta$ tại $K,Q$ sao cho $KQ = 4.$

3) Một cát tuyến đi qua $A\left( { - 1;\,\,4} \right)$ cắt $\left( C \right)$ tại $M,N$  sao cho diện tích tam giác $IMN$ có giá trị lớn nhất. Tìm giá trị lớn nhất đó.

4) Viết phương trình đường tròn $\left( {C'} \right)$có tâm $A\left( { - 1;\,\,4} \right)$ và cắt đường tròn $\left( C \right)$ tại $L,P$ sao cho $LP = 4.$

Câu 5 ( 1,0 điểm).

Viết phương trình chính tắc của elip $\left( E \right)$  đi qua điểm $N\left( {\frac{{3\sqrt 2 }}{2}; - \sqrt 2 } \right)$ và độ dài trục nhỏ là $4$.

Lời giải chi tiết

Bài 1 (VD)

Phương pháp:

1) Xét các trường hợp $x \ge  - 1$ và $x <  - 1$ để bỏ dấu giá trị tuyệt đối và giải bất phương trình.

2) Tìm ĐKXĐ sau đó giải bất phương trình: $\sqrt {f\left( x \right)}  \ge \sqrt {g\left( x \right)}  + \sqrt {h\left( x \right)}$ $\Leftrightarrow f\left( x \right) \ge {\left( {\sqrt {g\left( x \right)}  + \sqrt {h\left( x \right)} } \right)^2}.$

Cách giải:

1) ${x^2} + 3x - 1 + \left| {x + 1} \right| \le 0\,\,\,\left( * \right)$

+) Với $x \ge  - 1$ ta có:

$\begin{array}{l}\left( * \right) \Leftrightarrow {x^2} + 3x - 1 + x + 1 \le 0\\ \Leftrightarrow {x^2} + 4x \le 0\\ \Leftrightarrow x\left( {x + 4} \right) \le 0\\ \Leftrightarrow  - 4 \le x \le 0.\end{array}$

Kết hợp với $x \ge  - 1,$ ta có $- 1 \le x \le 0.$

+) Với $x <  - 1$ ta có:

 $\begin{array}{l}\left( * \right) \Leftrightarrow {x^2} + 3x - 1 - x - 1 \le 0\\ \Leftrightarrow {x^2} + 2x - 2 \le 0\\ \Leftrightarrow  - 1 - \sqrt 3  \le x \le  - 1 + \sqrt 3 .\end{array}$

Kết hợp với $x <  - 1,$ ta có $- 1 - \sqrt 3  \le x <  - 1.$

Vậy nghiệm của bất phương trình là $- 1 - \sqrt 3  \le x \le 0.$

2) $\sqrt {4x + 1}  - \sqrt {3 - x}  \ge \sqrt {2x}$

Điều kiện xác định: $0 \le x \le 3.$

$\begin{array}{l}\,\,\,\,\,\,\,\,\sqrt {4x + 1}  - \sqrt {3 - x}  > \sqrt {2x} \\ \Leftrightarrow \sqrt {4x + 1}  > \sqrt {2x}  + \sqrt {3 - x} \\ \Leftrightarrow 4x + 1 > 2x + 2\sqrt {2x} .\sqrt {3 - x}  + 3 - x\\ \Leftrightarrow 3x - 2 > 2\sqrt {2x} .\sqrt {3 - x} \\ \Leftrightarrow \left\{ \begin{array}{l}3x - 2 > 0\\{\left( {3x - 2} \right)^2} > 4\left( {6x - 2{x^2}} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > \frac{2}{3}\\9{x^2} - 12x + 4 > 24x - 8{x^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > \frac{2}{3}\\17{x^2} - 36x + 4 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > \frac{2}{3}\\\left( {x - 2} \right)\left( {17x - 2} \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > \frac{2}{3}\\\left[ \begin{array}{l}x > 2\\x < \frac{2}{{17}}\end{array} \right.\end{array} \right. \Leftrightarrow x > 2.\end{array}$

Kết hợp với điều kiện ta có nghiệm của bất phương trình là $2 < x \le 3.$

Bài 2 (VDC)

Phương pháp:

Đặt ẩn phụ đưa về bất phương trình bậc hai.

Sử dụng bất đẳng thức Cauchy để tìm khoảng giá trị của ẩn, sau đó vẽ bảng biến thiên đưa ra kết luận.

Cách giải:

Tìm tất cả các giá trị của m để bất phương trình sau: $\sqrt {3 + x}  + \sqrt {6 - x}  - \sqrt {(3 + x)(6 - x)}$$\le m$ đúng $\forall x \in \left[ { - 3;6} \right].$

$\sqrt {3 + x}  + \sqrt {6 - x}  - \sqrt {(3 + x)(6 - x)}$$\le m\,\,\,\,\left( * \right)$

Điều kiện: $- 3 \le x \le 6.$

Đặt $\sqrt {3 + x}  + \sqrt {6 - x}  = a \ge 0.$

$\begin{array}{l} \Rightarrow {a^2} = {\left( {\sqrt {3 + x}  + \sqrt {6 - x} } \right)^2}\\ = 9 + 2\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)}  \ge 9\\ \Rightarrow {a^2} \ge 9 \Rightarrow a \ge 3.\end{array}$

Áp dụng bất đẳng thức Cauchy cho hai số không âm $\sqrt {3 + x}$ và $\sqrt {6 - x}$ ta có:

$2\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)}  \le 3 + x + 6 - x$$= 9$

$\Rightarrow {a^2} \le 9 + 9 = 18 \Rightarrow a \le 3\sqrt 2 .$

Vậy $3 \le a \le 3\sqrt 2 .$

Ta có:

$\begin{array}{l}{a^2} = 9 + 2\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} \\ \Rightarrow \sqrt {\left( {3 + x} \right)\left( {6 - x} \right)}  = \frac{{{a^2} - 9}}{2}.\end{array}$

Bất phương trình trở thành: $a - \frac{{{a^2} - 9}}{2} \le m$ $\Leftrightarrow m \ge \frac{{ - {a^2} + 2a + 9}}{2}.$

Xét hàm số $f\left( a \right) =  - {a^2} + 2a + 9$ với $3 \le a \le 3\sqrt 2 .$

Ta có bảng biến thiên:

Từ bảng biến thiên suy ra $f\left( a \right) \le 6$ với $3 \le a \le 3\sqrt 2 .$

Vậy để $\sqrt {3 + x}  + \sqrt {6 - x}  - \sqrt {(3 + x)(6 - x)}  \le m$ đúng $\forall x \in \left[ { - 3;6} \right]$ thì $m \ge \frac{{\max f\left( a \right)}}{2} \Leftrightarrow m \ge 3.$

Bài 3 (VD)

Phương pháp:

1) Sử dụng công thức ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$ và với $\alpha  \in \left( {\pi ;\,\,2\pi } \right)$ ta có: $\sin \alpha  < 0.$

2) Sử dụng công thức: $\left\{ \begin{array}{l}\cos 2x = 2{\cos ^2}x - 1 = 1 - 2{\sin ^2}x\\\sin 2x = 2\sin x\cos x\end{array} \right..$

3) Sử dụng công thức: $\tan x = \frac{{\sin x}}{{\cos x}}.$

Cách giải:

1) Cho $\cos \alpha  = \frac{1}{3};\alpha  \in \left( {\pi ;2\pi } \right)$ tính giá trị$\sin \alpha  =$? Và  $A = \frac{{1 - 4{{\sin }^2}x + {{\cos }^2}x}}{{3 + {{\sin }^2}x - 4\cos 2x}}.$

Ta có với $\alpha  \in \left( {\pi ;\,\,2\pi } \right)$ ta có: $\sin \alpha  < 0.$

${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

$\Rightarrow {\sin ^2}\alpha  = 1 - {\cos ^2}\alpha$$= 1 - \frac{1}{{{3^2}}} = \frac{8}{9}.$

$\Rightarrow \sin \alpha  =  - \sqrt {\frac{8}{9}}  =  - \frac{{2\sqrt 2 }}{3}.$

$\begin{array}{l} \Rightarrow A = \frac{{1 - 4{{\sin }^2}x + {{\cos }^2}x}}{{3 + {{\sin }^2}x - 4\cos 2x}}\\ = \frac{{1 - 4{{\sin }^2}x + {{\cos }^2}x}}{{3 + {{\sin }^2}x - 4\left( {{{\cos }^2}x - {{\sin }^2}x} \right)}}\\ = \frac{{1 - 4.\frac{8}{9} + \frac{1}{3}}}{{3 + \frac{8}{9} - 4\left( {\frac{1}{3} - \frac{8}{9}} \right)}}\\ = \frac{{ - \frac{{20}}{9}}}{{\frac{{55}}{9}}} =  - \frac{4}{{11}}.\end{array}$

2) Chứng minh đẳng thức: $\frac{{1 + \sin 2x + \cos 2x}}{{1 + \sin 2x - \cos 2x}} = \cot x,$ với điều kiện biểu thức có nghĩa.

$\begin{array}{l}\frac{{1 + \sin 2x + \cos 2x}}{{1 + \sin 2x - \cos 2x}}\\ = \frac{{1 + 2\sin x\cos x + 2{{\cos }^2}x - 1}}{{1 + 2\sin x\cos x - \left( {1 - 2{{\sin }^2}x} \right)}}\\ = \frac{{2\sin x\cos x + 2{{\cos }^2}x}}{{2\sin x\cos x + 2{{\sin }^2}x}}\\ = \frac{{2\cos x\left( {\sin x + \cos x} \right)}}{{2\sin x\left( {\sin x + \cos x} \right)}}\\ = \cot x\,\,\,\,\left( {dpcm} \right).\end{array}$

3) Chứng minh tam giác $ABC$ vuông nếu: $\frac{{\cos C}}{{\sin C - \cos A}} = \tan B.$

Điều kiện: $\sin C - \cos A \ne 0,\cos B \ne 0.$

$\begin{array}{l}\frac{{\cos C}}{{\sin C - \cos A}} = \tan B\\ \Rightarrow \frac{{\cos C}}{{\sin C - \cos A}} = \frac{{\sin B}}{{\cos B}}\\ \Rightarrow \cos C.\cos B = \sin B.\sin C - \sin B.\cos A\\ \Rightarrow \cos C.\cos B - \sin C.\sin B =  - \sin B.\cos A\\ \Rightarrow \cos \left( {C + B} \right) =  - \sin B.\cos A\\ \Rightarrow  - \cos A =  - \sin B.\cos A\\ \Rightarrow \left[ \begin{array}{l}\cos A = 0\\\sin B = 1\,\end{array} \right. \Rightarrow \left[ \begin{array}{l}\angle A = 90^\circ \\\angle B = 90^\circ \end{array} \right..\end{array}$

Trường hợp $\angle A = 90^\circ$ không thỏa mãn do khi đó $\cos B = 0,$ trái với điều kiện.

Vậy $\frac{{\cos C}}{{\sin C - \cos A}} = \tan B$ thì tam giác ABC vuông tại A.

Bài 4 (VD)

Phương pháp:

1) Đường tròn $\left( C \right):\,\,\,{x^2} + {y^2} - 2ax - 2by + c = 0$  có tâm $I\left( {a;\,\,b} \right)$ và bán kính $R = \sqrt {{a^2} + {b^2} - c} .$

Ta xét điểm $B\left( {0;\,\,8} \right)$ thấy điểm $B$ thuộc đường tròn $\left( C \right).$

Khi đó tiếp tuyến của đường tròn $\left( C \right)$ tại $B$  đi qua $B$ và nhận $\overrightarrow {IB}$ làm VTPT.

2) Giả sử đường thẳng $d$ cắt đường tròn $\left( C \right)$ có tâm $I$ và bán kính $R$  theo dây cung $AB.$

Khi đó áp dụng định lý Pitago ta có: ${R^2} = {d^2}\left( {I;\,\,d} \right) + {\left( {\frac{{AB}}{2}} \right)^2}.$

Từ đó tìm được bán kính của đường tròn $\left( {C'} \right)$ và lập phương trình đường tròn.

3) Xác định diện tích $\Delta IMN$ sau đó áp dụng bất đẳng thức Cauchy để tìm giá trị lớn nhất.

4) Ta có $I,\,\,I'$ lần lượt là tâm của $\left( C \right),\,\,\left( {C'} \right)$ và $R,\,\,R'$ là bán kính của $\left( C \right),\,\,\left( {C'} \right).$

$\left( C \right)$ cắt $\left( {C'} \right)$ theo dây cung $LQ$ là có $LQ \bot II'$ tại $D$ là trung điểm của $LQ.$

Cách giải:

Trong hệ tọa độ$Oxy,$ cho đường tròn $\left( C \right):\,\,{x^2} + {y^2} + 6x - 8y = 0$ và điểm $A\left( { - 1;4} \right)$ và đường thẳng $\Delta :2x - y + 1 = 0$

1) Xác định tọa độ tâm $I$ và bán kính của đường tròn $\left( C \right)$. Viết phương trình tiếp tuyến của đường tròn $\left( C \right)$ tại điểm $B\left( {0;8} \right).$

$\left( C \right):\,\,{x^2} + {y^2} + 6x - 8y = 0$ có tâm $I\left( { - 3;\,\,4} \right)$ và bán kính $R = \sqrt {{3^2} + {4^2}}  = 5.$

Dễ thấy điểm $B\left( {0;8} \right)$ thuộc đường tròn $\left( C \right)$.

Có $\overrightarrow {IB} \left( {3;4} \right)$ là một vectơ pháp tuyến của tiếp tuyến với đường tròn $\left( C \right)$ tại điểm $B\left( {0;8} \right).$

$\Rightarrow$ Tiếp tuyến của $\left( C \right)$ tại $B\left( {0;\,\,8} \right)$  có phương trình là: $3\left( {x - 0} \right) + 4\left( {y - 8} \right) = 0$ $\Leftrightarrow 3x + 4y - 32 = 0$

2) Viết phương trình đường tròn $\left( {C'} \right)$ có tâm $A\left( { - 1;\,\,4} \right)$ và cắt đường thẳng $\Delta$ tại $K,Q$ sao cho $KQ = 4.$

Ta có: $d\left( {A;\,\,\Delta } \right) = \frac{{\left| {2.\left( { - 1} \right) - 4 + 1} \right|}}{{\sqrt {{2^2} + 1} }} = \frac{5}{{\sqrt 5 }} = \sqrt 5 .$

Đường tròn $\left( {C'} \right)$ cắt đường thẳng $\Delta$ tại hai điểm $K,\,\,Q$ với $KQ = 4,$ ta có bán kính $R'$ của $\left( {C'} \right)$ được xác định theo công thức:

$R' = \sqrt {{d^2}\left( {A;\,\,\Delta } \right) + {{\left( {\frac{{KQ}}{2}} \right)}^2}}$ $= \sqrt {5 + {{\left( {\frac{4}{2}} \right)}^2}}  = 3.$

Vậy phương trình đường tròn $\left( {C'} \right)$: ${\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 9.$

3) Một cát tuyến đi qua $A\left( { - 1;\,\,4} \right)$ cắt $\left( C \right)$ tại $M,N$  sao cho diện tích tam giác $IMN$ có giá trị lớn nhất. Tìm giá trị lớn nhất đó.

Ta có: $\overrightarrow {IA}  = \left( {2;\,\,0} \right)$ $\Rightarrow IA = 2 < R = \sqrt 5$

$\Rightarrow A$ nằm trong đường tròn $\left( C \right).$

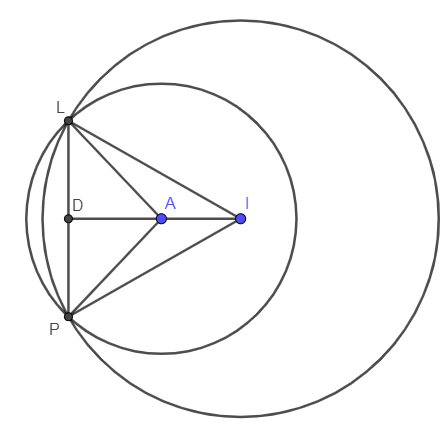
Ta có $IA = 2$.

Gọi $D$  là giao điểm của $IA$  với $LP$  thì $IA$  là trung trực của $LP \Rightarrow DL = \frac{1}{2}LP = 2.$  

Áp dụng định lý Pitago cho $\Delta IDL$ vuông tại $D$ ta có:

$I{D^2} + L{D^2} = I{L^2}$ $\Rightarrow ID = \sqrt {25 - 4}  = \sqrt {21}$$\Rightarrow AD = ID - AI = \sqrt {21}  - 2$

Áp dụng định lý Pitago cho $\Delta ALD$ vuông tại $D$ ta có:

$R{'^2} = A{L^2} = A{D^2} + D{L^2}$ $= {\left( {\sqrt {21}  - 2} \right)^2} + 4 = 29 - 4\sqrt {21}$

Vậy phương trình đường tròn $\left( {C'} \right)$cần tìm là: ${\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 29 - 4\sqrt {21} .$ 

Bài 5 (VD) - Phương trình đường elip

Phương pháp:

Gọi phương trình elip $\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$.

Khi đó độ dài trục nhỏ là: $2b.$

Từ độ dài trục nhỏ, tìm ra $b$, sau đó thay tọa độ điểm $N$ vào phương trình để tìm $a.$ 

Cách giải:

Viết phương trình chính tắc của elip $\left( E \right)$  đi qua điểm $N\left( {\frac{{3\sqrt 2 }}{2}; - \sqrt 2 } \right)$ và độ dài trục nhỏ là $4$.

Gọi elip $\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ trong đó ${a^2} - {b^2} = {c^2},\,\,\,a > b > 0.$

Độ dài trục nhỏ là $4 \Rightarrow 2b = 4 \Rightarrow b = 2$

$\Rightarrow \left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{2^2}}} = 1.$

Elip $\left( E \right)$  đi qua điểm $N\left( {\frac{{3\sqrt 2 }}{2}; - \sqrt 2 } \right)$

$\Rightarrow \frac{{\frac{9}{2}}}{{{a^2}}} + \frac{2}{{{2^2}}} = 1$

$\begin{array}{l} \Leftrightarrow \frac{9}{{2{a^2}}} = \frac{1}{2} \Leftrightarrow {a^2} = 9\\ \Rightarrow a = 3\,\,\,\left( {do\,\,\,a > 0} \right).\end{array}$

Vậy $\left( E \right):\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1.$

Nguồn: Sưu tầm

 HocTot.Nam.Name.Vn