Đề số 6 - Đề thi vào lớp 10 môn Toán

Đề bài

Câu 1. (2.5 điểm)

a)  Rút gọn các biểu thức

\(A = \sqrt {12}  + \sqrt {27}  - \sqrt {48} \)

\(B = \left( {\dfrac{1}{{\sqrt x  - 1}} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{x + 1}}{{x - 1}}\)  với \(x \ge 0\)  và \(x \ne  \pm 1\)

b)  Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 12\\3x - y = 1\end{array} \right.\)

Câu 2. (2 điểm)

Cho phương trình \({x^2} + 5x + m = 0\left( * \right)\) (m là tham số )

a)  Giải phương trình (*) khi \(m =  - 3\)

b)  Tìm m để phương trình (*) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(9{x_1} + 2{x_2} = 18\)

Câu 3. (2 điểm)

Trong mặt phẳng tọa độ \(\left( {Oxy} \right),\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;y = \left( {2m - 1} \right)x + 5.\)

a) Vẽ đồ thị của (P).

b) Tìm m để đường thẳng (d) đi qua điểm \(E\left( {7;\;12} \right).\)

c) Đường thẳng \(y = 2\) cắt parabol \(\left( P \right)\) tại hai điểm \(A,\;B.\) Tìm tọa độ của \(A,\;B\) và tính diện tích tam giác \(OAB.\)

Câu 4. (3,5 điểm)

Cho đường tròn tâm \(\left( {O;R} \right)\) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn \(\left( {O;R} \right)\) sao cho đoạn thẳng AC cắt đường tròn \(\left( {O;R} \right)\) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E.

a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.

b) Chứng minh CA.CK = CE.CH

c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.

d) Khi KE = KC. Chứng minh OK // MN.

Lời giải chi tiết

Câu 1.

a) Rút gọn các biểu thức

\(\begin{array}{l}A = \sqrt {12}  + \sqrt {27}  - \sqrt {48} \\\,\,\,\,\, = \sqrt {{2^2}.3}  + \sqrt {{3^2}.3}  - \sqrt {{4^2}.3} \\\,\,\,\,\, = 2\sqrt 3  + 3\sqrt 3  - 4\sqrt 3 \\\,\,\,\,\, = \sqrt 3 .\end{array}\)

\(B = \left( {\dfrac{1}{{\sqrt x  - 1}} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{x + 1}}{{x - 1}}\) với \(x \ge 0\)  và \(x \ne  \pm 1\)

\(\begin{array}{l}B = \left( {\dfrac{{\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} - \dfrac{{\sqrt x  - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right):\dfrac{{x + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\\;\; = \dfrac{{\sqrt x  + 1 - \sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}.\dfrac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{x + 1}}\\\;\; = \dfrac{2}{{x + 1}}.\end{array}\)

b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 12\\3x - y = 1\end{array} \right.\)

\(\left\{ \begin{array}{l}x + 2y = 12\\3x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y = 12\\y = 3x - 1\end{array} \right.\)

\(\Leftrightarrow \left\{ \begin{array}{l}x + 2\left( {3x - 1} \right) = 12\\y = 3x - 1\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}7x = 14\\y = 3x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5\end{array} \right.\)

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\;y} \right) = \left( {2;\;5} \right).\)

Câu 2.

Cho phương trình \({x^2} + 5x + m = 0\left( * \right)\) (m là tham số )

a) Giải phương trình (*) khi \(m =  - 3\)

Thay \(m =  - 3\) vào phương trình (*) ta có: \({x^2} + 5x - 3 = 0\)

Ta có: \(a = 1;b = 5;c =  - 3;\)

\(\Delta  = {b^2} - 4ac = {5^2} + 12 = 37 > 0\)

Khi đó phương trình có 2 nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 5 - \sqrt {37} }}{2}\\{x_2} = \dfrac{{ - 5 + \sqrt {37} }}{2}\end{array} \right.\)

Vậy khi \(m =  - 3\) thì phương trình (*)  có tập nghiệm là: \(S = \left\{ {\dfrac{{ - 5 - \sqrt {37} }}{2};\dfrac{{ - 5 + \sqrt {37} }}{2}} \right\}\)

b) Tìm m để phương trình (*) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(9{x_1} + 2{x_2} = 18\,\,\,\left( 3 \right)\)

+) Phương trình (*) có hai nghiệm \({x_1},{x_2}\) khi và chỉ khi \(\Delta  \ge 0 \Leftrightarrow 25 - 4m \ge 0 \Leftrightarrow m \le \dfrac{{25}}{4}\)

+) Áp dụng hệ thức Vi-et cho phương trình (*) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 5\,\,\left( 1 \right)\\{x_1}.{x_2} = m\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Kết hợp (1) và (3) ta được hệ phương trình:

\(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 5\\9{x_1} + 2{x_2} = 18\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}2{x_1} + 2{x_2} =  - 10\\9{x_1} + 2{x_2} = 18\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l} - 7{x_1} =  - 28\\{x_2} =  - 5 - {x_1}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 4\\{x_2} =  - 9\end{array} \right.\)

Thay \({x_1} = 4;{x_2} =  - 9\) vào (2) ta được: \(4.\left( { - 9} \right) = m \Leftrightarrow m =  - 36\left( {tm} \right)\)

Vậy \(m =  - 36\)  thỏa mãn yêu cầu bài toán.

Câu 3:

Trong mặt phẳng tọa độ \(\left( {Oxy} \right),\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;y = \left( {2m - 1} \right)x + 5.\)

a) Vẽ đồ thị của (P).

Ta có bảng giá trị:

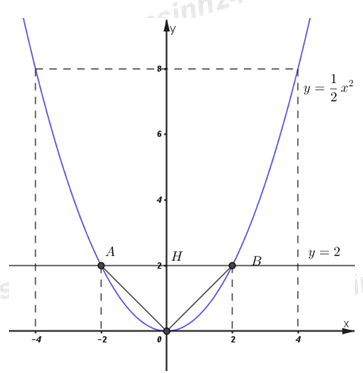
Đồ thị:

b) Tìm m để đường thẳng (d) đi qua điểm \(E\left( {7;\;12} \right).\)

Đường thẳng \(\left( d \right)\) đi qua điểm \(E\left( {7;\;12} \right) \Rightarrow 12 = \left( {2m - 1} \right).7 + 5\)

\(\begin{array}{l} \Leftrightarrow 12 = 14m - 7 + 5\\ \Leftrightarrow 14m = 14\\ \Leftrightarrow m = 1.\end{array}\)

Vậy \(m = 1\) thỏa mãn điều kiện bài toán.

c) Đường thẳng \(y = 2\) cắt parabol \(\left( P \right)\) tại hai điểm \(A,\;B.\) Tìm tọa độ của \(A,\;B\) và tính diện tích tam giác \(OAB.\)

Phương trình hoành độ giao điểm của đường thẳng \(y = 2\) và parabol \(\left( P \right)\) là:

\(\dfrac{1}{2}{x^2} = 2 \Leftrightarrow {x^2} = 4 \)

\(\Leftrightarrow \left[ \begin{array}{l}x =  - 2\\x = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A\left( { - 2;\;2} \right)\\B\left( {2;\;2} \right)\end{array} \right..\)

Đường thẳng \(y = 2\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( { - 2;\;2} \right)\) và \(B\left( {2;\;2} \right).\)

Gọi \(H\) là giao điểm của đường thẳng \(y = 2\) và trục \(Oy \Rightarrow H\left( {0;\;2} \right).\)

Khi đó ta có: \({S_{AOB}} = {S_{AOH}} + {S_{OBH}}.\)

Ta có: \(\left\{ \begin{array}{l}{S_{AOH}} = \dfrac{1}{2}AH.OH = \dfrac{1}{2}.\left| {{x_A}} \right|.\left| {{y_H}} \right| = \dfrac{1}{2}.2.2 = 2\\{S_{BOH}} = \dfrac{1}{2}HB.OH = \dfrac{1}{2}.\left| {{x_B}} \right|.\left| {{y_H}} \right| = \dfrac{1}{2}.2.2 = 2\end{array} \right..\)

\({S_{AOB}} = {S_{AOH}} + {S_{OBH}} = 2 + 2 = 4.\)

Vậy diện tích tam giác \(OAB\) là \(4\;\left( {dvdt} \right).\)

Câu 4.

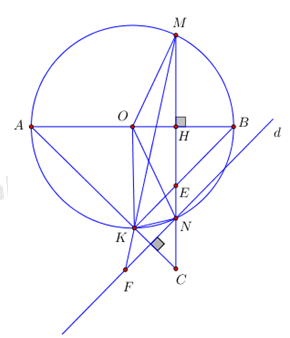
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.

Ta có \(\widehat {AKB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {AKE} = {90^0}\).

Xét tứ giác AHEK có \(\widehat {AKE} + \widehat {AHE} = {90^0} + {90^0} = {180^0} \Rightarrow \) tứ giác AHEK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰).

b) Chứng minh CA.CK = CE.CH

Xét tam giác CKE và tam giác CHA có:

\(\widehat {CKE} = \widehat {CHA} = {90^0};\)

\(\widehat {ACH}\) chung;

\( \Rightarrow \Delta CKE \sim \Delta CHA\,\,\left( {g.g} \right) \)

\(\Rightarrow \dfrac{{CK}}{{CH}} = \dfrac{{CE}}{{CA}} \)

\(\Rightarrow CA.CK = CE.CH\) (đpcm).

c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.

Ta có \(d \bot AC;\,\,\widehat {AKB} = {90^0} \Rightarrow BK \bot AK\)

\(\Rightarrow BK \bot AC \Rightarrow d//BK\). (từ vuông góc đến song song).

Xét tam giác OMN có 

\(OM = ON\left( { = R} \right) \Rightarrow \Delta OMN\) cân tại O.

\( \Rightarrow \) Đường cao OH đồng thời là đường phân giác \( \Rightarrow \widehat {MOB} = \widehat {NOB} \Rightarrow \) sđ cung MB = sđ cung NB.

\( \Rightarrow \widehat {MKB} = \widehat {NKB}\) (hai góc nội tiếp chắn hai cung bằng nhau).

Ta có \(\widehat {KFN} = \widehat {MKB}\) (đồng vị);

\(\widehat {KNF} = \widehat {NKB}\) (so le trong);

Mà \(\widehat {MKB} = \widehat {NKB}\,\,\left( {cmt} \right)\)

\(\Rightarrow \widehat {KFN} = \widehat {KNF} \)

\(\Rightarrow \Delta NEK\) cân tại K.

d) Khi KE = KC. Chứng minh OK // MN.

Ta có \(\widehat {AKB} = {90^0} \Rightarrow BK \bot AK \Rightarrow BK \bot AC \Rightarrow \Delta KEC\) vuông tại K.

Lại có KE = KC (gt) \( \Rightarrow \Delta KEC\) vuông cân tại K \( \Rightarrow \widehat {KEC} = {45^0}\) ;

\( \Rightarrow \widehat {HEB} = \widehat {KEC} = {45^0}\) (đối đỉnh) \( \Rightarrow \Delta HEB\) vuông cân tại H \( \Rightarrow \widehat {HBE} = {45^0} \Rightarrow \widehat {OBK} = {45^0}\)

Tam giác OBK có \(OB = OK\;\left( { = R} \right) \Rightarrow \Delta OBK\) cân tại O \( \Rightarrow \widehat {OBK} = \widehat {OKB} = {45^0}\)

\( \Rightarrow \widehat {BOK} = {180^0} - {45^0} - {45^0} = {90^0} \Rightarrow \Delta BOK\) vuông cân tại \(O \Rightarrow OK \bot OB\) ;

Lại có \(MN \bot AB\,\,\left( {gt} \right) \Rightarrow MN \bot OB\).

Vậy MN // OK.

HocTot.Nam.Name.Vn