Đề số 4 - Đề kiểm tra học kì 1 - Toán 9Tải vềĐáp án và lời giải chi tiết Đề số 4 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
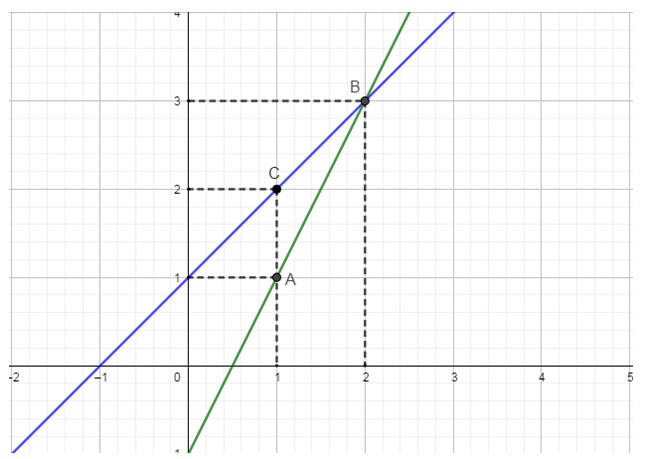
Đề bài Bài 1: (2 điểm) Thực hiện phép tính: a) \(A = 3\sqrt {32} - 6\sqrt 2 - \sqrt {50} \) b) \(B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \) Bài 2: (2 điểm) Cho đường thẳng \(\left( {{d_1}} \right):y = 2x - 1\) và đường thẳng \(\left( {{d_2}} \right):y = x + 1\) a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ. b) Tìm tọa độ giao điểm \(B\) của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép toán. Bài 3: (1 điểm) Rút gọn biểu thức sau a) \(C = \dfrac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 \) b) \(D = \left( {4 - \sqrt {15} } \right){\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)^2}\) Bài 4: (1 điểm) Nhân ngày “Black Friday” (24/11/2017). Một cửa hàng điện tử thực hiện giảm giá 50% trên một tivi trong lô hàng gồm 40 cái tivi với giả bán lẻ ban đầu là 6.500.000 đ/cái. Đến trưa cùng ngày đã bán được 20 cái, khi đó cửa hàng quyết định giảm thêm 10% nữa trên giá đang bán cho mỗi tivi thì bán được hết lô hàng. Biết rằng giá vốn là 3.050.000 đ/một tivi. Hỏi cửa hàng đó lời hay lỗ khi bán hết lô hàng tivi? Bài 5: (1 điểm) Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m , người ta nhìn thấy đỉnh núi với góc nắng lần lượt là \({34^o}\) và \({38^o}\). Bài 6: (1 điểm) Hiện nay tại nước Mỹ quy định cầu thang cho người khuyết tật dùng xe lăn có hệ số góc không quá \(\dfrac{1}{{12}}\). Để phù hợp với tiêu chuẩn ấy thì chiều cao cầu thang tối đa là bao nhiêu khi biết đáy của cầu thang có độ dài là 4m ? Bài 7: (2 điểm) Cho nửa đường tròn \(\left( O \right)\)đường kính \(AB\). Vẽ các tiếp tuyến \(Ax,By\). Từ một điểm M trên nửa đường tròn vẽ tiếp tuyến với \(\left( O \right)\) cắt \(Ax,By\) lần lượt tại D, C. a) Chứng minh: \(CD = AD + BC\) và \(\angle COD = {90^o}\). b) Gọi N là giao điểm của AC và BD. Chứng minh MN vuông góc với AB. LG bài 1 Lời giải chi tiết: a) \(A = 3\sqrt {32} - 6\sqrt 2 - \sqrt {50} \) \(A = 3\sqrt {32} - 6\sqrt 2 - \sqrt {50} = 3.\sqrt {{4^2}.2} - 6\sqrt 2 - \sqrt {{5^2}.2} = 3.4\sqrt 2 - 6\sqrt 2 - 5\sqrt 2 = \sqrt 2 \) Vậy \(A = \sqrt 2 \) b) \(B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \) \(B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} = \left| {5 + \sqrt 3 } \right| + \left| {2 - \sqrt 3 } \right| = 5 + \sqrt 3 + 2 - \sqrt 3 = 7\) Vậy \(B = 7\) LG bài 2 Lời giải chi tiết: Bài 2: Cho đường thẳng \(\left( {{d_1}} \right):y = 2x - 1\) và đường thẳng \(\left( {{d_2}} \right):y = x + 1\) a)Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ. Ta có: +) Hai điểm \(A\left( {1;1} \right),B\left( {2;3} \right)\) thuộc đồ thị hàm số \(\left( {{d_1}} \right):y = 2x - 1\) +) Hai điểm \(B\left( {2;3} \right),C\left( {1;2} \right)\) thuộc đồ thị hàm số \(\left( {{d_2}} \right):y = x + 1\) Từ đó ta có đồ thị của hai hàm số: b)Tìm tọa độ giao điểm \(A\) của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép toán. Hoành độ giao điểm là nghiệm của phương trình: \(2x - 1 = x + 1 \Leftrightarrow x = 2\) Với \(x = 2 \Rightarrow y = x + 1 = 3\) Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(B\left( {2;3} \right)\).
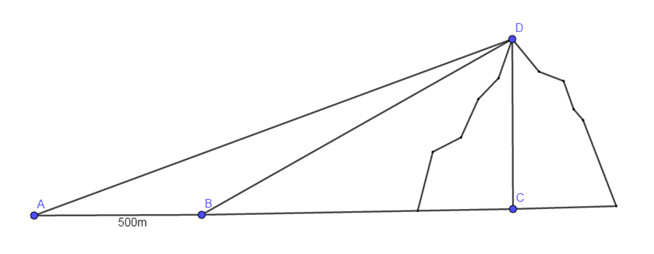
LG bài 3 Lời giải chi tiết: a) \(C = \dfrac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 \) \(C = \dfrac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 = \dfrac{{\sqrt 7 .\sqrt 2 + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 = \dfrac{{\sqrt 7 \left( {\sqrt 2 + 1} \right)}}{{\sqrt 2 + 1}} - \sqrt 7 = \sqrt 7 - \sqrt 7 = 0\) Vậy \(C = 0\) b)\(D = \left( {4 - \sqrt {15} } \right){\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)^2}\) \(\begin{array}{l}D = \left( {4 - \sqrt {15} } \right){\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)^2} \\= \dfrac{1}{4}.\left[ {2.\left( {4 - \sqrt {15} } \right)} \right].\left[ {{{\left( {\sqrt 2 } \right)}^2}{{\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)}^2}} \right]\\ = \dfrac{1}{4}\left( {8 - 2\sqrt {15} } \right){\left( {\sqrt {4 - 2\sqrt 3 } + \sqrt {6 + 2\sqrt 5 } } \right)^2}\\ = \dfrac{1}{4}.\left[ {{{\left( {\sqrt 3 } \right)}^2} - 2\sqrt 3 .\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}} \right].{\left( {\sqrt {{{\left( {\sqrt 3 } \right)}^2} - 2\sqrt 3 + 1} + \sqrt {{{\left( {\sqrt 5 } \right)}^2} + 2\sqrt 5 + 1} } \right)^2}\\ = \dfrac{1}{4}{\left( {\sqrt 5 - \sqrt 3 } \right)^2}.{\left( {\sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} + \sqrt {{{\left( {\sqrt 5 + 1} \right)}^2}} } \right)^2}\\ = \dfrac{1}{4}{\left( {\sqrt 5 - \sqrt 3 } \right)^2}.{\left( {\left| {\sqrt 3 - 1} \right| + \left| {\sqrt 5 + 1} \right|} \right)^2}\\ = \dfrac{1}{4}{\left( {\sqrt 5 - \sqrt 3 } \right)^2}{\left( {\sqrt 5 + \sqrt 3 } \right)^2}\\ = \dfrac{1}{4}{\left( {{{\left( {\sqrt 5 } \right)}^2} - {{\left( {\sqrt 3 } \right)}^2}} \right)^2} = \dfrac{1}{4}{.2^2} = 1\end{array}\) Vậy \(D = 1\) LG bài 4 Lời giải chi tiết: Bài 4:Nhân ngày “Black Friday” (24/11/2017). Một cửa hàng điện tử thực hiện giảm giá 50% trên một tivi trong lô hàng gồm 40 cái tivi với giả bán lẻ ban đầu là 6.500.000 đ/cái. Đến trưa cùng ngày đã bán được 20 cái, khi đó cửa hàng quyết định giảm thêm 10% nữa trên giá đang bán cho mỗi tivi thì bán được hết lô hàng. Biết rằng giá vốn là 3.050.000 đ/một tivi. Hỏi cửa hàng đó lời hay lỗ khi bán hết lô hàng tivi? Sau khi giảm giá 50% thì giá một chiếc tivi là: \(6500000.50\% = 3250000\) đ Vì đến trưa cửa hàng bán được 20 cái tivi nên ta có số tiền thu được là:\(3250000.20 = 65000000\)đ Vì số tivi chưa bán hết nên cửa hàng quyết định giảm thêm 10% nữa trên giá đang bán cho mỗi tivi , giá bán sau đó của mỗi tivi là: \(3250000.\left( {100\% - 10\% } \right) = 2925000\) đ Vì sau khi giảm giá thì bán được hết 20 cái tivi còn lại nên số tiền thu về là: \(2925000.20 = 58500000\) đ Vậy tổng số tiền thu được khi bán hết tivi là: \(65000000 + 58500000 = 123500000\) đ Tổng số tiền nhập tivi là: \(3050000.40 = 122000000\) đ Xét hiệu \(123500000 - 122000000 = 1500000\) đ Vì số tiền thu về lớn hơn số tiền nhập hàng nên cửa hàng đó lời khi bán hết 40 cái tivi với số tiền lời là 1500000 đ. LG bài 5 Lời giải chi tiết: Bài 5:Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m , người ta nhìn thấy đỉnh núi với góc nắng lần lượt là \({34^o}\) và \({38^o}\). Ta có hình vẽ minh họa
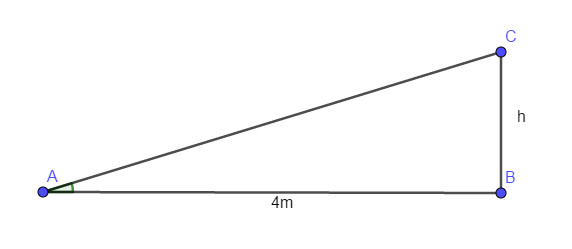
Xét tam giác vuông ADC vuông tại C có: \(\tan \left( {\angle DAC} \right) = \dfrac{{DC}}{{AC}} \Rightarrow AC = \dfrac{{DC}}{{\tan \left( {\angle DAC} \right)}}\). Xét tam giác vuông BDC vuông tại C có: \(\tan \left( {\angle DBC} \right) = \dfrac{{DC}}{{BC}} \Rightarrow BC = \dfrac{{DC}}{{\tan \left( {\angle DBC} \right)}}\). Có: \(\begin{array}{l}AC - BC = AB = 500\left( m \right) \Rightarrow \dfrac{{DC}}{{\tan \left( {\angle DAC} \right)}} - \dfrac{{DC}}{{\tan \left( {\angle DBC} \right)}} = 500\\ \Rightarrow DC.\left( {\dfrac{1}{{\tan {{34}^o}}} - \dfrac{1}{{\tan {{38}^o}}}} \right) = 500 \Rightarrow DC = \dfrac{{500}}{{\dfrac{1}{{\tan {{34}^o}}} - \dfrac{1}{{\tan {{38}^o}}}}} = 2468\left( m \right)\end{array}\) Vậy độ cao của ngọn núi là 2468 (m) LG bài 6 Lời giải chi tiết: Bài 6:Hiện nay tại nước Mỹ quy định cầu thang cho người khuyết tật dùng xe lăn có hệ số góc không quá \(\dfrac{1}{{12}}\). Để phù hợp với tiêu chuẩn ấy thì chiều cao cầu thang tối đa là bao nhiêu khi biết đáy của cầu thang có độ dài là 4m ? Ta có hình vẽ minh hoạ
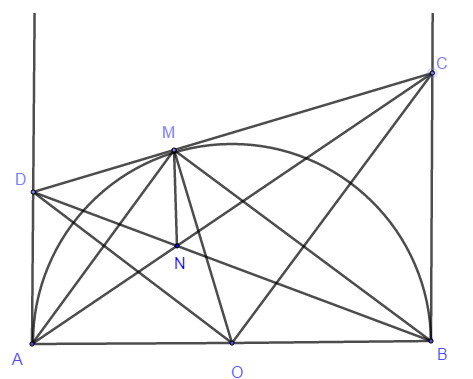
Gọi \(h\) là chiều cao tối đa của cầu thang. \(AB = 4\left( m \right)\) là độ dài đáy. Xét tam giác vuông ABC vuông tại B có: \(\tan \left( {\angle BAC} \right) = \dfrac{{BC}}{{AC}} = \dfrac{h}{4}\) Mà có hệ số góc là tan của góc tạo bởi cầu thang với mặt phẳng nằm ngang chính là \(\tan \left( {\angle BAC} \right)\) \( \Rightarrow h = 4.\tan \left( {\angle BAC} \right) = 4.\dfrac{1}{{12}} = \dfrac{1}{3}\left( m \right)\) Vậy chiều cao tối đa của thang là \(h = \dfrac{1}{3}\left( m \right)\) LG bài 7 Lời giải chi tiết: Bài 7:Cho nửa đường tròn \(\left( O \right)\)đường kính \(AB\). Vẽ các tiếp tuyến \(Ax,By\). Từ một điểm M trên nửa đường tròn vẽ tiếp tuyến với \(\left( O \right)\) cắt \(Ax,By\) lần lượt tại D, C.
a)Chứng minh: \(CD = AD + BC\) và \(\angle COD = {90^o}\). +) Xét đường tròn \(\left( O \right)\) có MD, AD là tiếp tuyến với A, M là tiếp điểm \( \Rightarrow AD = MD\) ( tính chất tiếp tuyến) (1) Chứng minh tương tự có \(MC = BC\) (2) Vì M nằm trên cạnh CD nên ta có: \(CD = MC + MD\) (3) Từ (1), (2), (3) ta có \(CD = AD + BC\) (đpcm) +) Xét tứ giác ADMO có: \(\angle DMO + \angle DAO = {90^o} + {90^o} = {180^o}\) (do DM, DA là tiếp tuyến với đường tròn) Suy ra tứ giác ADMO nội tiếp đường tròn. Xét đường tròn ngoại tiếp tứ giác ADMO có: \(\angle MDO,\angle MAO\)là hai góc nội tiếp cùng chắn cung MO, suy ra \(\angle MDO = \angle MAO\) Chứng minh tương tự có: \(\angle MCO = \angle MBO\) Xét tam giác AMB vuông tại M có: \(\angle MAO + \angle MBO = {90^o} \Rightarrow \angle MDO + \angle MCO = {90^o}\) Suy ra tam giác DOC vuông tại O, suy ra \(\angle COD = {90^o}\)(đpcm) b)Gọi N là giao điểm của AC và BD. Chứng minh MN vuông góc với AB. Xét tam giác BNC có AD song song với BC \( \Rightarrow \dfrac{{AD}}{{BC}} = \dfrac{{DN}}{{NB}}\) ( định lí Ta-lét trong tam giác) Mà có: \(\left\{ \begin{array}{l}AD = DM\\BC = MC\end{array} \right.\) (cmt) Suy ra \(\dfrac{{DM}}{{MC}} = \dfrac{{DN}}{{NB}}\). Xét tam giác BDC có: \(\dfrac{{DM}}{{MC}} = \dfrac{{DN}}{{NB}}\)\( \Rightarrow MN//BC\) ( định lí Ta-lét đảo) Mà có: \(BC \bot AB\) (do BC là tiếp tuyến với đường tròn) Suy ra \(MN \bot AB\) (đpcm) Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại HocTot.Nam.Name.Vn HocTot.Nam.Name.Vn
|