Đề số 17 - Đề kiểm tra học kì 1 - Toán 9Tải vềĐáp án và lời giải chi tiết Đề số 17 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài I. TRẮC NGHIỆM (1 điểm)Trả lời câu hỏi bằng cách viết lại chữ cái trước đáp án đúng vào bài làm: Câu 1 : Nếu x thỏa mãn điều kiện \(\sqrt {3 + \sqrt x } = 2\) thì x nhận giá trị là: A. 0 B. 4 C. 5 D. 1 Câu 2 : Điều kiện để hàm số bậc nhất \(y = \left( {1 - m} \right)x + m\,\,\left( {m \ne 1} \right)\)là hàm số nghịch biến là: A. \(m > 1\) B. \(m \ge 1\) C. \(m \le 1\) D. \(m < 1\) Câu 3 : Cho tam giác MNP vuông tại M, đường cao MH. Chọn hệ thức sai: A. \(M{H^2} = HN.HP\) B. \(M{P^2} = NH.HP\) C. \(MH.NP = MN.MP\) D. \(\dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}} = \dfrac{1}{{M{H^2}}}\) Câu 4 : Cho hai đường tròn \(\left( {I;7cm} \right)\)và \(\left( {K;5cm} \right)\). Biết \(IK = 2cm\). Quan hệ giữa hai đường tròn là: A. Tiếp xúc trong B. Tiếp xúc ngoài C. Cắt nhau D. Đựng nhau II. TỰ LUẬN (9 điểm) Câu 1 (1 điểm):Thực hiện phép tính: a) \(3\sqrt {\dfrac{1}{3}} + 4\sqrt {12} - 5\sqrt {27} \) b) \(\dfrac{{3 + 2\sqrt 3 }}{{\sqrt 3 }} - \dfrac{2}{{\sqrt 3 - 1}}\) Câu 2 (2 điểm): Cho biểu thức \(P = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}\,\,\left( {x \ge 0;x \ne 4} \right)\) a) Rút gọn P b) Tìm x sao cho \(P = 2\) c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \dfrac{1}{4}\) Câu 3 (2 điểm):Cho hàm số \(y = \left( {m - 4} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\)\(\left( {m \ne 4} \right)\). a) Tìm m để đồ thị hàm số đi qua \(A\left( {1;6} \right)\) b) Vẽ đồ thị hàm số với m tìm được ở câu a. Tính góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox (làm tròn đến phút). c) Tìm m để đường thẳng \(\left( d \right)\) song song với đường thẳng\(\left( {{d_1}} \right):y = \left( {m - {m^2}} \right)x + m + 2\) Câu 4 (3,5 điểm):Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn \(\left( O \right)\) (với E là tiếp điểm). Vẽ dây EH vuông góc với AO tại M. a) Cho biết bán kính \(R = 5cm,\,\,OM = 3cm\). Tính độ dài dây EH. b) Chứng minh AH là tiếp tuyến của đường tròn\(\left( O \right)\). c) Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn \(\left( O \right)\) (F là tiếp điểm). Chứng minh 3 điểm E, O, F thẳng hàng và \(BF.AE = {R^2}\). d) Trên tia HB lấy điểm I (\(I \ne B\)), qua I vẽ tiếp tuyến thứ hai với đường tròn \(\left( O \right)\) cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắtAE tại Q. Chứng minh \(AE = DQ\). Câu 5 (0,5 điểm):Cho x,y là các số thực dương thỏa mãn \(x + y \le 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \left( {\dfrac{1}{x} + \dfrac{1}{y}} \right).\sqrt {1 + {x^2}{y^2}} \). LG trắc nghiệm Lời giải chi tiết: I. TRẮC NGHIỆM
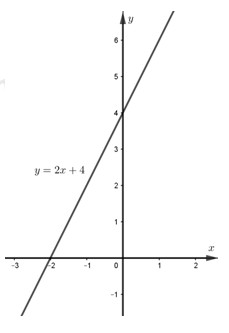
LG bài 1 Lời giải chi tiết: a) \(3\sqrt {\dfrac{1}{3}} + 4\sqrt {12} - 5\sqrt {27} = \sqrt 3 + 8\sqrt 3 - 15\sqrt 3 = - 6\sqrt 3 \) b) \(\dfrac{{3 + 2\sqrt 3 }}{{\sqrt 3 }} - \dfrac{2}{{\sqrt 3 - 1}} = \dfrac{{\left( {\sqrt 3 + 2} \right)\sqrt 3 }}{{\sqrt 3 }} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \sqrt 3 + 2 - \sqrt 3 - 1 = 1\) LG bài 2 Lời giải chi tiết: Cho biểu thức \(P = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}\,\,\left( {x \ge 0;x \ne 4} \right)\) a) Rút gọn P \(\begin{array}{l}P = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\\\;\;\; = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\\;\; = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{\sqrt x }}{{\sqrt x + 2}} = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\end{array}\) b) Tìm x sao cho \(P = 2\) \(P = 2 \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} = 2 \) \(\Leftrightarrow \sqrt x = 2\sqrt x - 4 \) \(\Leftrightarrow \sqrt x = 4 \Leftrightarrow x = 16\) c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \dfrac{1}{4}\) \(M = P:Q = \dfrac{{\sqrt x }}{{\sqrt x - 2}}.\dfrac{{\sqrt x - 2}}{{\sqrt x + 2}} = \dfrac{{\sqrt x }}{{\sqrt x + 2}}\) \({M^2} < \dfrac{1}{4} \Leftrightarrow {\left( {\dfrac{{\sqrt x }}{{\sqrt x + 2}}} \right)^2} < \dfrac{1}{4} \) \(\Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x + 2}} < \dfrac{1}{2}\) \(\Leftrightarrow 2\sqrt x < \sqrt x + 2 \Leftrightarrow \sqrt x < 2 \Leftrightarrow x < 4\) Kết hợp điều kiện đầu bài \( \Rightarrow 0 \le x < 4\) LG bài 3 Lời giải chi tiết: Cho hàm số \(y = \left( {m - 4} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\)\(\left( {m \ne 4} \right)\). a) Tìm m để đồ thị hàm số đi qua \(A\left( {1;6} \right)\) \(A\left( {1;\;6} \right)\) thuộc đường thẳng \(\left( d \right).\) Ta thay \(x = 1;\,\,y = 6\) vào hàm số \(y = \left( {m - 4} \right)x + 4\) ta được \(6 = \left( {m - 4} \right).1 + 4 \Leftrightarrow m = 6\;\;\left( {tm} \right)\) Vậy với\(m = 6\) thì đồ thị hàm số đi qua \(A\left( {1;6} \right)\) b) Vẽ đồ thị hàm số với m tìm được ở câu a. Tính góc tạo bởi đồ thị hàm số vừa vẽ với trục Ox (làm tròn đến phút). Với \(m = 6\) thì \(y = 2x + 4\) Ta có bảng giá trị:
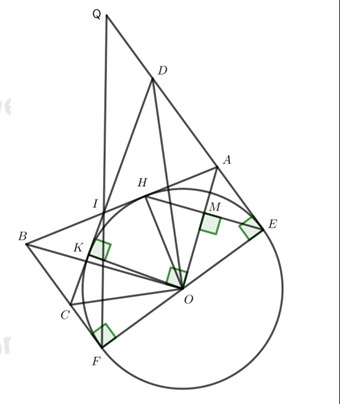
Đường thẳng \(y = 2x + 4\) đi qua hai điểm \(\left( {0;4} \right)\) và \(\left( { - 2;0} \right)\) Gọi \(\alpha \) là góc tạo bởi đồ thị hàm số vừa vẽ với trụcOx \( \Rightarrow \tan \alpha = 2 \Rightarrow \alpha \approx {63^o}{26'}\) c) Tìm m để đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {{d_1}} \right):y = \left( {m - {m^2}} \right)x + m + 2\) \(\left( d \right)//\left( {{d_1}} \right) \Leftrightarrow \left\{ \begin{array}{l}m - {m^2} = m - 4\\m + 2 \ne 4\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{m^2} = 4\\m \ne 2\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = - 2\;\;\left( {tm} \right)\) Vậy với \(m = - 2\) thỏa mãn yêu cầu đề bài. LG bài 4 Lời giải chi tiết: Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn \(\left( O \right)\) (với E là tiếp điểm). Vẽ dây EH vuông góc với AO tại M.
a) Cho biết bán kính \(R = 5cm,\,\,OM = 3cm\). Tính độ dài dây EH. Theo đề bài ta có: \(EH \bot OA\) tại M nên M là trung điểm của EH hay \(EH = 2EM\)(định lý mối liên hệ giwuax đường kính và dây cung) Áp dụng định lý Pi-ta-go cho tam giác vuông OME có: \(EM = \sqrt {O{E^2} - O{M^2}} = \sqrt {{5^2} - {3^2}} = 4\) Vậy \(EH = 2EM = 8\,\,(cm)\) b) Chứng minh AH là tiếp tuyến của đường tròn \(\left( O \right)\). Ta có \(\left\{ \begin{array}{l}OA \bot EH\\ME = MH\end{array} \right. \Rightarrow \)OA là đường trung trực của EH\( \Rightarrow AE = AH\) Xét hai tam giác OEA và tam giác OHA có: \(OE = OH\,\,( = R);\,\,\,AE = AH;\,\,OA\)chung \( \Rightarrow \Delta OEA = \Delta OHA\)(c.c.c) \( \Rightarrow \angle OHA = \angle OEA = {90^o}\) hay \(AH \bot OH\) Vậy AH là tiếp tuyến của \(\left( O \right)\) (đpcm). c) Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn \(\left( O \right)\) (F là tiếp điểm). Chứng minh 3 điểm E, O, F thẳng hàng và \(BF.AE = {R^2}\). Có \(AH \bot OH\;\;\left( {cmt} \right)\) hay Blà giao của hai tiếp tuyến BH; BF \( \Rightarrow \angle BOF = \angle BOH\), lại có \(\angle EOA = \angle HOA\) \( \Rightarrow \angle EOA + \angle AOB + \angle BOF = 2\left( {\angle AOH + \angle BOH} \right) = 2\angle AOB = {180^o}\) \( \Rightarrow \)E, O, F thẳng hàng. (đpcm) Có \(\angle EOA + \angle BOF = {180^o} - \angle AOB = {90^o} \Rightarrow \angle OAE = \angle BOF\) (cùng phụ \(\angle AOE\)) Xét \(\Delta AOE\) và \(\Delta OBF\)có: \(\angle OAE = \angle BOF\); \(\angle AEO = \angle BFO = {90^o}\) \( \Rightarrow \dfrac{{AE}}{{OF}} = \dfrac{{OE}}{{BF}} \Rightarrow AE.BF = OE.OF = {R^2}\,\,\,\,\,\left( 1 \right)\) d) Trên tia HB lấy điểm I (\(I \ne B\)), qua I vẽ tiếp tuyến thứ hai với đường tròn \(\left( O \right)\) cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q. Chứng minh \(AE = DQ\). Có \(BF//AQ\) (do cùng vuông góc với EF) \( \Rightarrow \dfrac{{BF}}{{CF}} = \dfrac{{AQ}}{{DQ}}\)(định lý Talet) (*) Dễ dàng chứng minh \(\Delta COD\) vuông tại O. Gọi K là tiếp điểm của tiếp tuyến thứ 2 qua I với \(\left( O \right)\) Áp dụng hệ thức lượng trong tam giác vuông COD đường cao DK ta có: \(O{K^2} = DK.CK\) Mà DE, DK là các tiếp tuyến của \(\left( O \right)\)cắt nhau tại D nên \(DE = DK\) Tương tự \(CK = CF \Rightarrow O{K^2} = CF.DE \Leftrightarrow CF.DE = {R^2}\,\,\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\)và \(\left( 2 \right)\) suy ra: \(CF.DE = AE.BF \Leftrightarrow \dfrac{{BF}}{{CF}} = \dfrac{{DE}}{{AE}}\) (**) Từ (*) và (**) suy ra: \(\dfrac{{AQ}}{{DQ}} = \dfrac{{DE}}{{AE}} \Leftrightarrow \dfrac{{AQ}}{{AQ - DQ}} = \dfrac{{DE}}{{DE - AE}} \Leftrightarrow \dfrac{{AQ}}{{AD}} = \dfrac{{DE}}{{AD}} \Leftrightarrow AQ = DE\) Câu 5: Cho x,y là các số thực dương thỏa mãn \(x + y \le 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \left( {\dfrac{1}{x} + \dfrac{1}{y}} \right).\sqrt {1 + {x^2}{y^2}} \). Có x, y là các số thực dương \( \Rightarrow \dfrac{1}{x};\dfrac{1}{y}\) là các số thực dương Áp dụng bất đẳng thức Cô-si ta được : \(\dfrac{1}{x} + \dfrac{1}{y} \ge 2\sqrt {\dfrac{1}{x}.\dfrac{1}{y}} = \dfrac{2}{{\sqrt {xy} }}\) Vậy \(P \ge \dfrac{2}{{\sqrt {xy} }}.\sqrt {1 + {x^2}{y^2}} = 2\sqrt {\dfrac{1}{{xy}} + xy} \) Ta có : \(1 \ge x + y \ge 2\sqrt {xy} \)(do x, y là hai số thực dương)\( \Rightarrow xy \le \dfrac{1}{4}\) \(\dfrac{1}{{xy}} + xy = \dfrac{1}{{16xy}} + xy + \dfrac{{15}}{{16}}.\dfrac{1}{{xy}} \ge 2\sqrt {\dfrac{1}{{16xy}}.xy} + \dfrac{{15}}{{16}}\dfrac{1}{{\dfrac{1}{4}}} = 2.\dfrac{1}{4} + \dfrac{{15}}{4} = \dfrac{{17}}{4}\) \( \Rightarrow P \ge 2\sqrt {\dfrac{{17}}{4}} = \sqrt {17} \). Dấu ‘=’ xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = y\\x + y = 1\\xy = \dfrac{1}{4}\end{array} \right. \Leftrightarrow x = y = \dfrac{1}{2}\) Vậy giá trị nhỏ nhất của P là \(\sqrt {17} \) đạt được khi \(x = y = \dfrac{1}{2}.\) Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại HocTot.Nam.Name.Vn HocTot.Nam.Name.Vn
|