Đề kiểm tra giữa học kì 1 môn toán lớp 7 năm 2020 - 2021 trường THCS Mỹ Đình 1Giải chi tiết đề kiểm tra giữa học kì 1 môn toán lớp 7 năm 2020 - 2021 trường THCS Mỹ Đình 1 với cách giải nhanh và chú ý quan trọng Đề bài I. Trắc nghiệm (2đ) Câu 1: Phân số biểu diễn số hữu tỉ 2−5 là:
Câu 2: Kết quả của phép tính (1112:3316).92 là:
Câu 3:Cho 20:x=4:5 giá trị của x bằng:
Câu 4: Từ tỉ lệ thức ab=cd với a,b,c,d≠0 có thể suy ra:
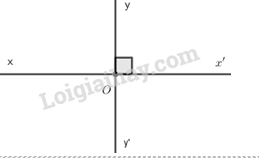
Câu 5: Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Chúng được gọi là hai đường thẳng vuông góc với nhau khi:
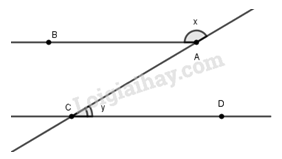
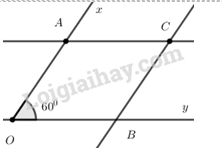
Câu 6: Cho ba đường thẳng phân biệt a,b,c. Hai đường thẳng a và b song song với nhau khi: A. a và b cùng cắt c B. a⊥c và b⊥c C. a cắt c và b⊥c D.a⊥c và b cắt c Câu 7: Cho hình vẽ trên và biết AB//CD thì: A. x=y B. y=1800+x C.y=x−1800 D.x+y=1800 Câu 8: Cho^xOy=600 . Trên ta Ox, Oy lần lượt lấy điểm A, B khác O. Từ A vẽ đường thẳng song song với OB, từ B vẽ đường thẳng song song với OA, chúng cắt nhau tại C. Khi đó số đo của ^ACB là:
II. Tự luận (8 điểm) Câu 1(1,5 điểm). Thực hiện phép tính (Tính nhanh nếu có thể): a) 1124−541+1324+0,5−3641 b) 1635.−13−1335.−13 c) 23+3.(−12)4−(−12)2.4+[(−2)2:12]:8 Câu 2 (1,5 điểm). Tìm x, biết: a) 14.x−13=−59 b) x−3x+5=57 c) 2x−3−3.2x=−92 Câu 3 (1,5 điểm). Tính số học sinh của lớp 7A và 7B biết số học sinh của lớp 7A ít hơn số học sinh lớp 7B là 5 học sinh và tỉ số học sinh 2 lớp là 8:9.
Câu 5 (0,5 điểm). Cho biểu thức: A=2+22+23+...+22020. Tìm x, biết: 2(A+2)=22x HẾT Lời giải chi tiết I.Trắc nghiệm
Câu 1: 2−5=2.2−5.2=4−10=−410 . Chọn đáp án A Câu 2: (1112:3316).92=1112.1633.92=11.4.2.2.3.34.3.3.11.2=2. Chọn đáp án B Câu 3: 20:x=4:5⇔20x=45⇔4.x=20.5⇔4x=100⇔x=25 Chọn đáp án D Câu 4: Theo giả thiết ta có: ab=cd⇔bc=ad Đáp án A: 3a2c=2d3b⇔9ab=4cd (loại) Đáp án B: 3ba=3dc⇔3bc=3ad⇔bc=ad (thỏa mãn) Đáp án C: 5a5d=bc⇔5ac=5bd⇔ac=bd ( loại) Đáp án D: a2b=d2c⇔2ac=2bd⇔ac=bd (loại) Câu 5:
Câu 6: a//b khi chúng cùng vuông góc với đường thẳng c Chọn đáp án B Câu 7: Do AB//CD nên x+^BAC=1800 (kề bù) Mà ^BAC=^ACD (So le trong) suy ra: x+^ACD=1800⇒x+y=1800 Chọn đáp án D Câu 8:
II. Tự luận Câu 1: a) 1124−541+1324+0,5−3641=(1124+1324)−(541+3641)+0,5=1−1+0,5=0,5 b) 1635.−13−1335.−13=−13.(1635−1335)=−13.3=−1 c) 23+3.(−12)4−(−12)2.4+[(−2)2:12]:8=8+3.116−14.4+(4:12):8=8+316−1+8:8=8+316=13116 Câu 2:
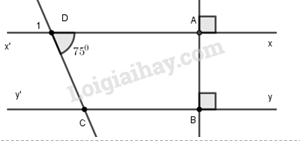
c) 2x−3−3.2x=−922x−3−3.23.2x−3=−922x−3−24.2x−3=−922x−3.(1−24)=−922x−3.(−23)=−922x−3=−92:(−23)2x−3=42x−3=22x−3=2x=5 Vậy x=5 Câu 3: Gọi số học sinh của lớp 7A và 7B lần lượt là x,y,z (x,y,z∈N∗) Do số học sinh lớp 7A ít hơn số học sinh lớp 7B là 5 học sinh nên ta có: y−x=5(1) Tỉ số học sinh của hai lớp là 8:9 nên x8=y9(2) Từ (1) và (2) ta có: x8=y9và y−x=5 Áp dụng tính chất dãy tỉ số bằng nhau ta có: x8=y9=y−x9−8=51=5 +) x8=5⇒x=5.8=40 +) y9=5⇒y=5.9⇒y=45 Vậy số học sinh của lớp 7A là 40 học sinh và 7B là 45 học sinh Câu 4: Ta có: xx′⊥AByy′⊥AB}⇒xx′//yy′ a) Ta có: ^D1=^ADC (đối đỉnh) mà ^ADC=750 nên ^D1=750 Vì xx' // yy' nên ^DCy+^ADC=1800 (2 góc trong cùng phía) ^DCy+750=1800^DCy=1050 b) Do Ct là phân giác của ^DCy nên: ^DCE=^DCy2=52,50 Xét tam giác DEC có: ^DCE+^CDE+^DEC=180052,50+750+^DEC=1800^DEC=52,50 Vậy ^DCE=^DEC Câu 5: A=2+22+23+...+220202A=22+23+24+...+22020+220212A−A=22021−2A=22021−2 Do đó, ta có: 2(A+2)=22x⇒2(22021−2+2)=22x2.22021=22x⇒22022=22x⇒2x=2022⇒x=1011 Vậy x=1011
|