Đề kiểm tra 45 phút - Đề số 5 - Chương 2 - Đại số 7Giải Đề kiểm tra 45 phút - Đề số 5 - Chương 2 - Đại số 7
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Bài 1: Một ô tô đi từ A đến B với vận tốc 45km/h hết 1 giờ. Hỏi nếu đi với vận tốc 60km/h thì mất bao lâu? Bài 2: Tam giác có chu vi 72cm và ba cạnh tỉ lệ thuận với 3,4,5. Tính độ dài ba cạnh. Bài 3: Cho hàm số \(y = kx.\) a) Tìm k biết nếu \(y = -5\) và \(y = {5 \over 2}\) b) Vẽ đồ thị của hàm số với k vừa tìm được c) Chứng tỏ ba điểm \(O ; A(1 ;-2); B(2;1)\) không thẳng hàng. LG bài 1 Phương pháp giải: Sử dụng tính chất hai đại lượng tỉ lệ nghịch - Tích của một giá trị bất kì của đại lượng này với giá trị tương ứng của đại lượng kia luôn là một hằng số (bằng hệ số tỉ lệ). \({x_1}{y_1} = {x_2}{y_2} = {x_3}{y_3} = ... = a\) Lời giải chi tiết: Gọi x là vận tốc của ô tô; y là thời gian ô tô đi hết quãng đường AB.(\(x,y > 0\); x bằng km/h; y tính bằng giờ). Ta có thể tóm tắt trong bảng dưới đây:
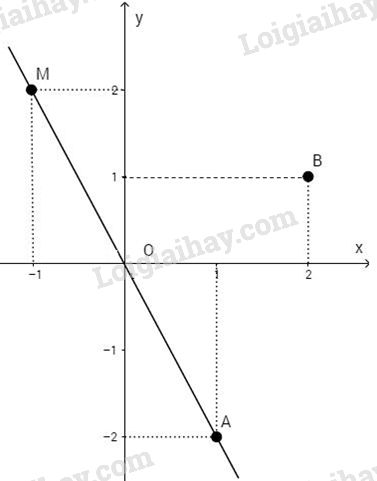
Vì x,y là hai đại lượng tỉ lệ nghịch, nên theo tính chất của đại lượng tỉ lệ nghịch, ta có: \({x_1}{y_1} = {x_2}{y_2};\) trong đó \({x_1} = 45;\) \({x_2} = 60;\)\({y_1} = 1\) \( \Rightarrow 45.1 = 60.{y_2} \Rightarrow {y_2} = {{45} \over {60}} = {3 \over 4}.\) Vậy ô tô đi 60km/h sẽ hết \({3 \over 4}\) (giờ) = (45 phút) LG bài 2 Phương pháp giải: Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c + e}}{{b + d + f}}\) Lời giải chi tiết: Gọi x; y; z là độ dài ba cạnh của tam giác (\(x,y,z > 0\) ;cm). Chu vi của tam giác bằng 72 nên ta có \(x + y + z = 72.\) Vì x, y, z tỉ lệ ( thuận) với ba số 3 ;4 ;5 nên ta có : \({x \over 3} = {y \over 4} = {z \over 5} = {{x + y + z} \over {3 + 4 + 5}} = {{72} \over {12}} = 6\) \( \Rightarrow {x \over 3} = 6 \Rightarrow x = 18;\) \({y \over 4} = 6 \Rightarrow y = 24;\) \({z \over 5} = 6 \Rightarrow z = 30\) Vậy ba cạnh của tam giác có độ dài: 18(cm) ;24(cm) ;30(cm). LG bài 3 Phương pháp giải: Đồ thị hàm số \(y = ax (a ≠ 0)\) là đường thẳng đi qua gốc toạ độ và \(A(1;a)\) Điểm \(M(x_0;y_0)\) thuộc đồ thị hàm số \(y=ax\) nếu \(y_0=ax_0\) Thay tọa độ các điểm A, B, C vào hàm số \(y=-2x\) để chỉ ra 3 điểm không thẳng hàng. Lời giải chi tiết: a) Thế \(y = -5\) và \(x = {5 \over 2}\) vào công thức \(y = kx\), ta được: \(-5 =k.{5 \over 2}\) \( \Rightarrow k = - 2\). Vậy \(y = -2x.\) b) Đồ thị của hàm số \(y = -2x\) là đường thằng qua hai điểm O và \(M(1 ;-2)\). (xem hình vẽ).
c) Thế tọa độ của A :\({x_A} = 1;y = - 2\) vào công thức \(y = -2x\), ta được : \( - 2 = ( - 2).1\) (luôn đúng). Vậy A thuộc đồ thị của hàm số. Thế tọa độ của B :\({x_B} = 2;{y_B} = 1\) vào công thức \(y = -2x\), ta được : \(1 = ( - 2).2\) (sai). Vậy B không thuộc đồ thị của hàm số. Mà đồ thị \(y=-2x\) là đường thẳng qua O, A. Vậy O, A, B không thẳng hàng (xem hình vẽ) HocTot.Nam.Name.Vn
|