Đề kiểm tra 45 phút - Đề số 4 - Chương 2 - Đại số 7Giải Đề kiểm tra 45 phút - Đề số 4 - Chương 2 - Đại số 7
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Bài 1: Có 496 học sinh được phân thành bốn loại : khá, giỏi , trung bình, và yếu. Số học sinh yếu chiếm 18 số học sinh. Còn lại số học sinh giỏi, khá, trung bình tỉ lệ thuận với các số 7,10,14. Hãy tính số học sinh từng loại. Bài 2: Hai xe ô tô cùng đi từ A đến B. Vận tốc của xe thứ nhất là 60km/h ; của xe thứ hai là 40km/h nên thời gian đi của xe thứ nhất ít dơn xe thứ hai là 30 phút. Tính quãng đường AB Bài 3: Cho hàm số y=f(x)=mx. a) Tìm m biết rằng f(−1)=12. b) Vẽ đồ thị hàm số với m vừa tìm được. c) Đánh dấu vị trí các điểm M(2;1);N(−2;1). Chứng tỏ rằng O ; M ; N thẳng hàng. LG bài 1 Phương pháp giải: Sử dụng tính chất dãy tỉ số bằng nhau ab=cd=ef=a+c+eb+d+f Lời giải chi tiết: Học sinh yếu chiếm 18 số học sinh nên số học sinh yếu là ta có : 496.18=62(em). Vậy số học sinh còn lại : 496−62=434 học sinh giỏi, khá và trung bình. Gọi x, y, z là số học sinh giỏi, khá và trung bình (x,y,z∈N∗ ). Vì có 434 học sinh giỏi, khá và trung bình nên x+y+z=434 Với x, y, z tỉ lệ ( thuận ) với 7 ; 10 ; 14 nên ta có: x7=y10=z14=x+y+z7+10+14=43431=14 ⇒x=14.7=98;y=14.10=140;z=14.14=196. Trả lời : Số học sinh giỏi, khá, trung bình, yếu lần lượt là 98 ;140 ;196 ;62 (em) LG bài 2 Phương pháp giải: Sử dụng tính chất hai địa lượng tỉ lệ nghịch: Tích của một giá trị bất kì của đại lượng này với giá trị tương ứng của đại lượng kia luôn là một hằng số (bằng hệ số tỉ lệ). x1y1=x2y2=x3y3=...=a Lời giải chi tiết: Gọi x là vận tốc (x > 0 ; km/h ); y là thời gian (y > 0; giờ). Ta có thể tóm tắt trong bảng như sau:
Ta có : x1y1=x2y2 (quãng đường AB). ⇒y1x2=y2x1 hay y140=y260=y2−y160−40=1220=140 30phút=12 (giờ) ⇒y1=1(giờ) Vậy x1.y1=60.1=60 Vậy quãng đường AB dài 60km LG bài 3 Phương pháp giải: Đồ thị hàm số y=ax(a≠0) là đường thẳng đi qua gốc toạ độ và A(1;a) Điểm M(x0;y0) thuộc đồ thị hàm số y=ax nếu y0=ax0 Thay tọa độ các điểm O, M, N vào hàm số y=−12x để chỉ ra 3 điểm thẳng hàng. Lời giải chi tiết: a) Ta có : f(−1)=12⇒m.(−1)=12 ⇒m=−12. Vậy y=f(x)=−12x.
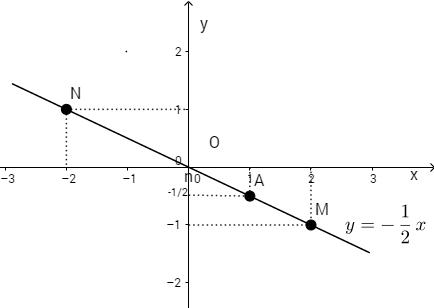
b) Đồ thị của hàm số y=−12x là đường thẳng qua gốc tọa độ và điểm A(1;12). (xem hình vẽ) c) Thế tọa độ của M : xM=2;yM=−12x ta được : −1=(−12).2 (luôn đúng). Vậy M thuộc đồ thị của hàm số y=−12x. Tương tự N cũng thuộc đồ thị này, mà đồ thị là đường thẳng đi qua O. Vậy O ; M ; N thẳng hàng. HocTot.Nam.Name.Vn
|