Đề kiểm tra 45 phút - Đề số 1 - Chương 2 - Đại số 7Giải Đề kiểm tra 45 phút - Đề số 1 - Chương 2 - Đại số 7
Lựa chọn câu để xem lời giải nhanh hơn
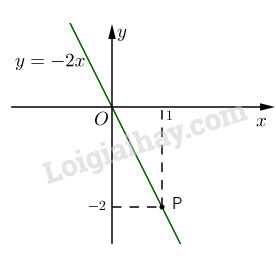
Đề bài Bài 1: Có ba loại tiền mệnh giá 2000 đồng; 5000 đồng và 10 000 đồng gồm 16 tờ. Biết rằng tổng giá trị của mỗi loại đều bằng nhau. Hỏi mỗi loại tiền có bao nhiêu tờ? Bài 2: Vẽ đồ thị của hàm số y=−2x . Điểm M(−5;10) có thuộc đồ thị của hàm số hay không? Chứng tỏ ba điểm O;A(−1;2) và B(2;−4) thẳng hàng. Bài 3: Cho tam giác ABC , biết rằng số đo ba góc A;B;C tỉ lệ thuận với 12;13;16 .Tìm số đo của ba góc A,B,C. Bài 4 : Cho hàm số y=f(x)=mx. Tìm m biết f(12)=2. LG bài 1 Phương pháp giải: Sử dụng tính chất dãy tỉ số bằng nhau ab=cd=ef=a+c+eb+d+f Lời giải chi tiết: Gọi x, y, z là số tờ tiền của loại tiền mệnh giá 2000 đồng và 5000 đồng và 10 000 đồng (x,y,z∈N∗) Vì có tất cả 16 tờ tiền nên ta có: x+y+z=16 Vì tổng giá trị của mỗi loại bằng nhau nên ta có : 2000x=5000y=10000z⇒2000x10000=5000y10000=10000z10000 ⇒x5=y2=z1=x+y+z5+2+1=168=2(Tính chất của dãy tỉ số bằng nhau) ⇒x=5.2=10;y=2.2=4;z=1.2=2 Vậy loại tiền 2000 đồng có 10 tờ, 5000 đồng có 4 tờ ; 10 000 đồng có 2 tờ. LG bài 2 Phương pháp giải: Đồ thị hàm số y=ax(a≠0) là đường thẳng đi qua gốc toạ độ và A(1;a) Thay tọa độ các điểm A, B, C vào hàm số y=−2x để chỉ ra 3 điểm thẳng hàng. Lời giải chi tiết: Đồ thị của hàm số y=−2x có đường thẳng qua gốc tọa độ O và điểm P(1;−2)
Thay tọa độ của điểm M(−5;10) vào hàm số y=−2x; với x=−5;y=10. Ta có : 10=(−2).(−5) hay 10=10 (luôn đúng). Vậy M thuộc đồ thị hàm số y=−2x. Tương tự, ta được A,B thuộc đồ thị hàm số y=−2x (là đường thẳng) Vậy O, A, B thẳng hàng. LG bài 3 Phương pháp giải: Sử dụng tính chất dãy tỉ số bằng nhau ab=cd=ef=a+c+eb+d+f Lời giải chi tiết: Trong tam giác ABC, ta có ˆA+ˆB+ˆC=1800. Vì ˆA,ˆB,ˆC tỉ lệ thuận với 12;13;16 . ˆA12=ˆB13=ˆC16=ˆA+ˆB+ˆC12+13+16=18001 ⇒ˆA=18002=900;ˆB=18003=600;ˆC=18006=300 Vậy ˆA=900;ˆB=600;ˆC=300. LG bài 4 Phương pháp giải: Thay x=12;y=2 vào hàm số để tìm m. Lời giải chi tiết: Ta có: f(x)=mx nên f(12)=m.12 Suy ra: f(12)=2⇒2=m.12⇒m=2:12=4. HocTot.Nam.Name.Vn
|