Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 2 - Đại số 9Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 2 - Đại số 9
Lựa chọn câu để xem lời giải nhanh hơn
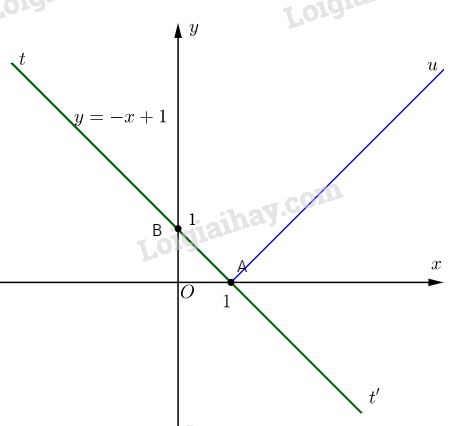
Đề bài Bài 1. Cho hai đường thẳng : \(y = (m – 1)x + 1\) (d1) và \(y = (2 – m)x + 2\) (d2) \((m ≠ 1, m ≠ 2)\) a. Tìm m để hai đường thẳng song song b. Chứng tỏ (d1) luôn đi qua 1 điểm cố định c. Tìm m để hàm số \(y = (2 – m)x + 2\) đồng biến trên \(\mathbb R\) d. Tìm m để (d2) qua điểm \(M(1; 2)\) Bài 2. Cho hàm số \(y = -x + 1\) a. Vẽ đồ thị của hàm số trên. Từ đó suy ra đồ thị của hàm số \( y = \left| { - x + 1} \right|\) b. Đồ thị của hàm số \(y = -x + 1\) cắt Ox, Oy lần lượt tại A và B. Tính diện tích tam giác OAB. LG bài 1 Phương pháp giải: a) Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau khi và chỉ khi \(a = a', b ≠ b'\). b) Đưa về phương trình ẩn m: \(Am+B=0\) đúng với mọi m khi \(A=0\) và \(B=0\) c) Hàm số \(y=ax+b\) đồng biến trên \(R\) khi \(a>0\) d) Thay tọa độ điểm M vào phương trình đường thẳng \((d_2)\) để tìm m. Lời giải chi tiết: a. (d1) // (d2) \( \Leftrightarrow \left\{ {\matrix{ {m - 1 = 2 - m} \cr {1 \ne 2} \cr } } \right. \Leftrightarrow m = {3 \over 2}\) b. Gọi \(A({x_0}{\rm{; }}{y_0})\) là điểm cố định cần tìm. (d1) qua A \( \Leftrightarrow {y_0} = \left( {m - 1} \right){x_0} + 1\) (với mọi m) \( \Leftrightarrow {x_0}m + 1 - {y_0} - {x_0} = 0\) (với mọi m) Phương trình bậc nhất của m có vô số nghiệm \( \Leftrightarrow \left\{ {\matrix{ {{x_0} = 0} \cr {1 - {y_0} - {x_0} = 0} \cr } } \right. \Leftrightarrow \left\{ {\matrix{ {{x_0} = 0} \cr {{y_0} = 1} \cr } } \right.\) Vậy \(A(0; 1)\). c. Hàm số \(y = (2 – m)x + 2\) đồng biến trên \(\mathbb R\) \(⇔ 2 – m > 0 ⇔ m < 2\) d. \(M ∈ (d_2)\)\(\; ⇔ 2 = (2 – m).1 + 2 ⇔ m = 2\) LG bài 2 Phương pháp giải: a) Xác định tọa độ 2 điểm thuộc đồ thị hàm số rồi vẽ đường thẳng đi qua hai điểm đó b) Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông Lời giải chi tiết: a. Bảng giá trị:
Đồ thị của hàm số là đường thẳng (d) qua hai điểm \(A(1; 0)\) và \(B(0; 1)\).
Ta có: \( \eqalign{ & \left| {1 - x} \right| \cr&= \left\{ {\matrix{ { - x + 1\,\text{ nếu }\, - x + 1 \ge 0} \cr { - \left( { - x + 1} \right)\,\text{ nếu }\, - x + 1 < 0} \cr } } \right. \cr & = \left\{ {\matrix{ { - x + 1\,\text{ nếu }\,x \le 1} \cr {x - 1\,\text{ nếu }\,x > 1} \cr } } \right. \cr} \) Vậy đồ thị của hàm số \( y = \left| { - x + 1} \right|\) được suy ra từ đồ thị của hàm số \(y = -x + 1\) bằng cách sau: + Tia At được giữ nguyên. + Lấy đối xứng tia At’ qua trục hoành, ta được đồ thị của hàm số \( y = \left| { - x + 1} \right|\) là đường gấp khúc tAu. b. Ta có: \( {S_{OAB}} = {1 \over 2}OA.OB = {1 \over 2}\) (đvdt) HocTot.Nam.Name.Vn
|