Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 2 - Đại số 9Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 2 - Đại số 9
Lựa chọn câu để xem lời giải nhanh hơn
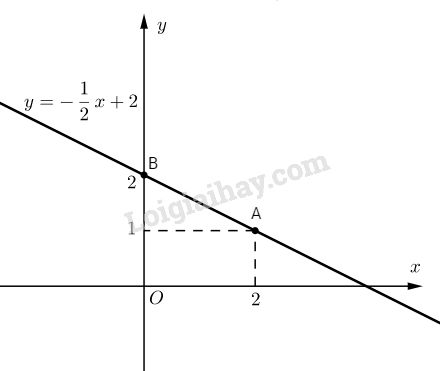
Đề bài Bài 1. Cho hàm số \(y = (m – 1)x + 2\) có đồ thị là đường thẳng (d). a. Tìm m biết (d) đi qua \(A(2; 1)\) và vẽ đồ thị với m vừa tìm được. b. Viết phương trình đường thẳng (d’) qua \(M(1; 3)\) và cắt trục tung tại điểm có tung độ bằng 5. Tìm tọa độ giao điểm của (d) và (d’) Bài 2. Cho hai đường thẳng : \(y = x – 1\) (d1) và \(y = -x + 3\) (d2) a. Vẽ hai đường thẳng trên cùng mặt phẳng tọa độ. b. Gọi M là giao điểm của (d1) và (d2). Viết phương trình đường thẳng qua M và O (O là gốc tọa độ). c. Tính góc α tạo bởi (d2) và trục Ox. LG bài 1 Phương pháp giải: a) Thay tọa độ điểm A vào hàm số để tìm m Xác định tọa độ 2 điểm thuộc đồ thị hàm số rồi vẽ đường thẳng đi qua hai điểm đó b) Viết phương trình đường thẳng (d') bằng cách: Xác định được tung độ gốc bằng 5 rồi thay tọa độ điểm M vào phương trình đường thẳng để tìm a. Giải phương trình hoành độ giao điểm để tìm x, từ đó thay vào một trong hai hàm số ban đầu để tìm y. Lời giải chi tiết: a. \(A \in \left( d \right) \Rightarrow 1 = 2\left( {m - 1} \right) + 2 \) \(\Rightarrow m = {1 \over 2}\) Ta có: \(y = - {1 \over 2}x + 2\) Đồ thị của hàm số là đường thẳng qua \(A(2; 1)\) và \(B(0; 2)\).
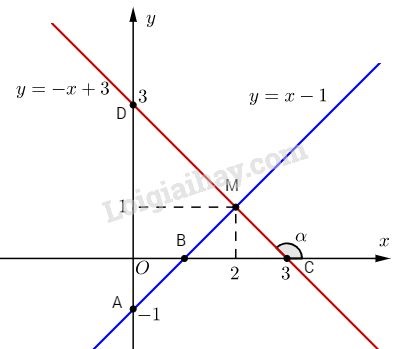
b. Phương trình (d’) có dạng: \(y = ax + b\; (a≠ 0)\) Vì (d’) cắt Oy tại điểm có tung độ bằng 5 nên \(b = 5\) Khi đó: \(y = ax + 5\) \(M \in \left( {d'} \right) \Rightarrow 3 = a + 5 \Rightarrow a = - 2\) Vậy phương trình (d’) : \(y = -2x + 5\) Phương trình hoành độ giao điểm của (d) và (d’): \( - {1 \over 2}x + 2 = - 2x + 5 \Leftrightarrow x = 2\) Thế \(x = 2\) vào phương trình của (d’), ta được \(y = 1\). Vậy tọa độ giao điểm là \((2; 1)\). LG bài 2 Phương pháp giải: a) Xác định tọa độ 2 điểm thuộc đồ thị hàm số rồi vẽ đường thẳng đi qua hai điểm đó b) Giải phương trình hoành độ giao điểm để tìm x, từ đó thay vào một trong hai hàm số ban đầu để tìm y. c) Tính góc dựa vào tỉ số lượng giác của góc nhọn. Lời giải chi tiết: a. Đường thẳng (d1) qua hai điểm \(A(0; -1)\) và \(B(1; 0).\) Đường thẳng (d2) qua hai điểm \(C(0; 3)\) và \(D(3; 0)\)
b. Phương trình hoành độ giao điểm của (d1) và (d2) : \(x – 1 = -x + 3 ⇔ x = 2\) Thế \(x = 2\) vào phương trình (d1) \(⇒ y = 1\). Vậy \(M(2; 1)\). Phương trình đường thẳng qua O có dạng : \(y = ax\) Đường thẳng này qua M \(⇒ 1 = a.2 \Rightarrow a = {1 \over 2}\) Vậy phương trình đường thẳng OM là : \(y = {1 \over 2}x\) c. Trong tam giác vuông OCD, ta có: \(OC = OD = 3\) \( \Rightarrow \tan \widehat {CDO} = {3 \over 3} = 1 \Rightarrow \widehat {CDO} = 45^\circ \) \(\Rightarrow \widehat {DCx} = 180^\circ - 45^\circ = 135^\circ \) Vậy \(\alpha = 135^\circ \) HocTot.Nam.Name.Vn
|