Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương III - Hình học 12Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương III - Hình học 12 Đề bài Câu 1: Trong không gian Oxyz cho ba vectơ →a=(3;−2;4),→b=(5;1;6), →c=(−3;0;2). Tìm vectơ →x sao cho vectơ →x đồng thời vuông góc với →a,→b,→c A. (1;0;0). B. (0;0;1). C. (0;1;0). D. (0;0;0). Câu 2: Trong không gianOxyz, cho 2 điểm B(1;2;−3),C(7;4;−2). Nếu E là điểm thỏa mãn đẳng thức →CE=2→EB thì tọa độ điểm E là A. (3;83;−83). B. (3;83;83). C. (3;3;−83). D. (1;2;13). Câu 3: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;−1), B(2;−1;3),C(−2;3;3). ĐiểmM(a;b;c) là đỉnh thứ tư của hình bình hành ABCM, khi đó P=a2+b2−c2 có giá trị bằng A.43.. B. 44.. C. 42.. D. 45. Câu 4: Trong không gian với hệ trục tọa độ Oxyzcho ba điểm A(1;2;−1), B(2;−1;3),C(−2;3;3). Tìm tọa độ điểmD là chân đường phân giác trong góc A của tam giácABC A. D(0;1;3). B. D(0;3;1). C. D(0;−3;1). D. D(0;3;−1). Câu 5: Trong không gian với hệ toạ độ Oxyz, cho các điểm: A(-1,3,5), B(-4,3,2), C(0,2,1). Tìm tọa độ điểm I tâm đường tròn ngoại tiếp tam giác ABC A. I(83;53;83). B. I(53;83;83). C. I(−53;83;83). D. I(83;83;53). Câu 6: Trong không gian Oxyz, cho 3 vectơ A. 13 B. 4 C. 23 D. 2 Câu 7: Trong không gian với hệ trục Oxyz cho tọa độ 4 điểm A(2;-1;1), B(1;0;0), C(3,1,0), D(0;2;1). Cho các mệnh đề sau: 1) Độ dài AB=√2. 2) Tam giác BCD vuông tại B. 3) Thể tích của tứ diện ABCD bằng 6. Các mệnh đề đúng là: A. 2). B. 3). C. 1); 3). D. 2), 1) Câu 8: Trong không gianOxyz, cho ba vectơ →a=(−1,1,0);→b=(1,1,0);→c=(1,1,1). Trong các mệnh đề sau, mệnh đề nào đúng: A. cos(→b,→c)=√63. B. →a+→b+→c=→0. A. →a,→b,→c đồng phẳng. D. →a.→b=1. Câu 9: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD, biết A(1;0;1),B(−1;1;2), C(−1;1;0), D(2;−1;−2). Độ dài đường cao AHcủa tứ diện ABCD bằng: A. 2√13. B. 1√13. C. √132. D. 3√1313. Câu 10: Cho hình chóp tam giác S.ABC với I là trọng tâm của đáy ABC. Đẳng thức nào sau đây là đẳng thức đúng A. →SI=12(→SA+→SB+→SC). B. →SI=13(→SA+→SB+→SC). C. →SI=→SA+→SB+→SC. D. →SI+→SA+→SB+→SC=→0. Câu 11: Phương trình mặt cầu tâm I(2;4;6) nào sau đây tiếp xúc với trục Ox: A. (x−2)2+(y−4)2+(z−6)2=20. B. (x−2)2+(y−4)2+(z−6)2=40. C. (x−2)2+(y−4)2+(z−6)2=52. D. (x−2)2+(y−4)2+(z−6)2=56. Câu 12: Mặt cầu tâm I(2;4;6) tiếp xúc với trục Oz có phương trình: A. (x−2)2+(y−4)2+(z−6)2=20. B. (x−2)2+(y−4)2+(z−6)2=40. C. (x−2)2+(y−4)2+(z−6)2=52. D. (x−2)2+(y−4)2+(z−6)2=56. Câu 13: Cho mặt cầu (S): (x−1)2+(y−2)2+(z−3)2=9. Phương trình mặt cầu nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua mặt phẳng (Oxy): A. (x+1)2+(y+2)2+(z+3)2=9. B. (x+1)2+(y−2)2+(z+3)2=9. C. (x−1)2+(y+2)2+(z+3)2=9. D. (x−1)2+(y−2)2+(z+3)2=9. Câu 14: Cho mặt cầu (S): (x+1)2+(y−1)2+(z−2)2=4. Phương trình mặt cầu nào sau đây là phương trình mặt cầu đối xứng với mặt cầu (S) qua trục Oz: A. (x−1)2+(y+1)2+(z−2)2=4. B. (x+1)2+(y+1)2+(z−2)2=4. C. (x−1)2+(y−1)2+(z−2)2=4. D. (x+1)2+(y−1)2+(z+2)2=4. Câu 15: Đường tròn giao tuyến của (S):(x−1)2+(y−2)2+(z−3)2=16 khi cắt bởi mặt phẳng (Oxy) có chu vi bằng: A. √7π. B. 2√7π. C. 7π. D. 14π. Câu 16: Trong không gian với hệ toạ độ Oxyz,tọa độ điểm M nằm trên trục Oy và cách đều hai mặt phẳng: (P):x+y−z+1=0 và (Q):x−y+z−5=0 là: A.M(0;−3;0). B.M(0;3;0). C.M(0;−2;0). D. M(0;1;0). Câu 17: Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng qua G(1;2;3) và cắt các trục Ox,Oy,Oz lần lượt tại các điểm A,B,C (khác gốc O) sao cho G là trọng tâm của tam giác ABC. Khi đó mặt phẳng (α) có phương trình: A.3x+6y+2z+18=0. B.6x+3y+2z−18=0. C.2x+y+3z−9=0. D.6x+3y+2z+9=0. Câu 18: Trong không gian với hệ toạ độ Oxyz, gọi (α)là mặt phẳng song song với mặt phẳng (β):2x−4y+4z+3=0 và cách điểm A(2;−3;4) một khoảng k=3. Phương trình của mặt phẳng (α) là: A.2x−4y+4z−5=0 hoặc 2x−4y+4z−13=0. B. x−2y+2z−25=0. C.x−2y+2z−7=0. D.x−2y+2z−25=0 hoặc x−2y+2z−7=0. Câu 19: Trong không gian với hệ toạ độ Oxyz,cho hai đường thẳng d1,d2lần lượt có phương trình d1:x−22=y−21=z−33, d2:x−12=y−2−1=z−14. Phương trình mặt phẳng (α) cách đều hai đường thẳng d1,d2 là: A.7x−2y−4z=0. B.7x−2y−4z+3=0. C. 2x+y+3z+3=0. D.14x−4y−8z+3=0. Câu 20: Trong không gian (x+4)2+(y+1)2+(z+6)2=18., cho mặt phẳng (x−4)2+(y−1)2+(z−6)2=9.: (x−4)2+(y−1)2+(z−6)2=16. và đường thẳng d:N(−5;7;0). Với giá trị nào của →u=(2;−2;1)thì →MN=(−9;6;−6)cắt H A.(S). B.(S) . C.R2=MH2+(AB2)2=18 . D.d(M,d)=3. Lời giải chi tiết
Câu 1: Dễ thấy chỉ có →x=(0;0;0)thỏa mãn →x.→a=→x.→b=→x.→c=0. Câu 2: E(x;y;z), từ →CE=2→EB⇒{x=3y=83z=−83. Câu 3: M(x;y;z), ABCM là hình bình hành thì →AM=→BC⇒{x−1=−2−2y−2=3+1z+1=3−3 ⇒M(−3;6;−1)⇒P=44.. Câu 4: Ta có AB=√26,AC=√26⇒ tam giác ABCcân ở A nên D là trung điểm BC ⇒D(0;1;3). Câu 5: Ta có: Tam giác đều. Do đó tâm I của đường tròn ngoại tiếp là trọng tâm của nó. Kết luận: I(−53;83;83) Câu 6: →OA=→a⇒A(−1;1;0),→OB=→b⇒B(1;1;0),→OC′=→c⇒C′(1;1;1). →AB=→OC⇒C(2;0;0)⇒→CC′=(−1;1;1)=→OO′ ⇒VOABC.O′A′B′C′=|[→OA,→OB]→OO′| Câu 8: cos(→b,→c)=→b.→c|→b|.|→c| Câu 9: Sử dụng công thức h=|[→AB,→AC].→AD||→AB.→AC|=1√13. Câu 10: →SI=→SA+→AI→SI=→SB+→BI→SI=→SC+→CI}⇒3→SI=→SA+→SB+→SB+(→AI+→BI+→CI) Vì I là trọng tâm tam giác ABC⇒→AI+→BI+→CI=→0 ⇒→SI=13(→SA+→SB+→SC). Câu 11: Mặt cầu tâm I(2;4;6), bán kính R và tiếp xúc trục Ox⇔R=d(I;Ox) ⇔R=√y2I+z2I=√52. Vậy (S):(x−2)2+(y−4)2+(z−6)2=52. Lựa chọn đáp án C. Câu 12: Mặt cầu tâm I(2;4;6), bán kính R và tiếp xúc trục Ox⇔R=d(I;Oz) ⇔R=√x2I+y2I=√20. Vậy (S):(x−2)2+(y−4)2+(z−6)2=20. Lựa chọn đáp án A. Câu 13: Mặt cầu (S) tâm I(1;2;3), bán kính R=3. Do mặt cầu (S′) đối xứng với (S) qua mặt phẳng (Oxy) nên tâm I' của (S′) đối xứng với I qua (Oxy), bán kính R′=R=3. Ta có : I′(1;2;−3). Vậy (S):(x−1)2+(y+2)2+(z−3)2=9. Lựa chọn đáp án D. Lưu ý: Để ý thấy rằng trung điểm II′ thuộc mặt phẳng (Oxy) và →II′⊥(Oxy). Cả 4 đáp án trên đều có thể dễ dàng tìm được tọa độ I′ nên nếu tinh ý ta sẽ tiết kiệm được thời gian hơn trong việc tìm đáp án. Câu 14: Mặt cầu (S) tâm I(−1;1;2), bán kính R=2. Do mặt cầu (S′) đối xứng với (S) qua trục Oz nên tâm I' của (S′) đối xứng với I qua trục Oz, bán kính R′=R=2. Ta có : I′(1;−1;2). Vậy (S):(x−1)2+(y+1)2+(z−2)2=4. Lựa chọn đáp án A. Câu 15: Mặt cầu (S) tâm I(1;2;3), bán kính R=4. Ta có : d(I;(Oxy))=|zI|=3. Gọi r là bán kính đường tròn (C) giao tuyến của mặt cầu (S) và mặt phẳng (Oxy), ta suy ra : r=√R2−[d(I;(Oxy))]2=√7. Vậy chu vi (C) bằng : 2√7π. Lựa chọn đáp án B. Câu 16: Ta có M∈Oy⇒M(0;m;0) Giả thiết có d(M,(P))=d(M,(Q))⇔|m+1|√3=|−m−5|√3⇔m=−3 Vậy M(0;−3;0) Câu 17: Gọi , , là giao điểm của mặt phẳng các trục Phương trình mặt phẳng (α) :xa+yb+zc=1 (a,b,c≠0) . Ta có G là trọng tâm tam giác ABC ⇒{a3=1b3=2c3=3⇔{a=3b=6c=9⇒(α):x3+y6+z9=1⇔6x+3y+2z−18=0 Câu 18: Vì (α)//(β)⇒(α):2x−4y+4z+m=0(m≠3) Giả thiết có d(A,(α))=3⇔|32+m|6=3⇔[m=−14m=−50 Vậy (α):x−2y+2z−7=0, (α):x−2y+2z−25=0 Câu 19: Ta có d1 đi qua A(2;2;3) và có →ud1=(2;1;3), d2 đi qua B(1;2;1) và có →ud2=(2;−1;4) →AB=(−1;1;−2);[→ud1;→ud2]=(7;−2;−4) ⇒[→ud1;\)\(→ud2]→AB=−1≠0 nên d1,d2 chéo nhau. Do (α) cách đều d1,d2 nên (α) song song với d1,d2⇒→nα=[→ud1;→ud2]=(7;−2;−4) ⇒(α) có dạng 7x−2y−4z+d=0 Theo giả thiết thì d(A,(α))=d(B,(α))⇔|d−2|√69=|d−1|√69⇔d=32 ⇒(α):14x−4y−8z+3=0 Câu 20:(x−4)2+(y−1)2+(z−6)2=18. có VTPT Oxyz x2+y2+z2−2x+4y−6z−11=0 có VTCP (P) 2x+2y−z−7=0cắt (Q) Chọn đáp án D. HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|













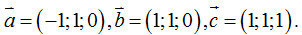 . Cho hình hộp
. Cho hình hộp 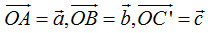 . Thể tích của hình hộp nói trên bằng:
. Thể tích của hình hộp nói trên bằng:







