Đề kiểm tra 45 phút (1 tiết) - Đề số 10 - Chương 2 - Hình học 9Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 10 - Chương 2 - Hình học 9
Lựa chọn câu để xem lời giải nhanh hơn
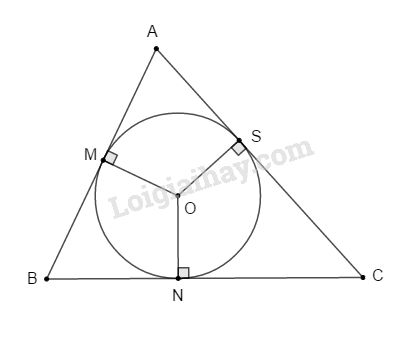
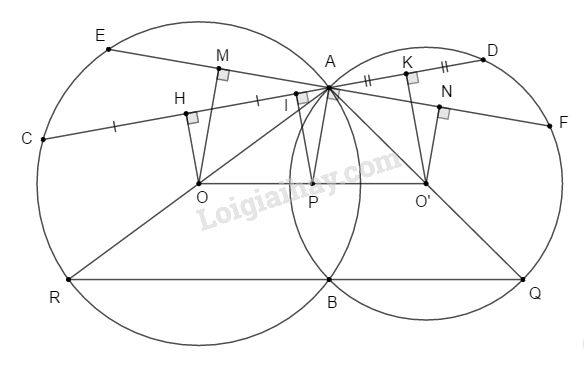
Đề bài Bài 1. Cho đường tròn (O) nội tiếp ∆ABC. Gọi M, N, S lần lượt là các tiếp điểm thuộc các cạnh AB, BC, CA. Chứng minh rằng : \(AB + AC – BC = 2AM.\) Bài 2. Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Một cát tuyến kẻ qua A cắt (O) tại C và cắt (O’) tại D. Gọi H, K lần lượt là trung điểm của AC và AD và I là trung điểm của HK. a. Chứng minh rằng đường thẳng vuông góc với CD tại I đi qua một điểm cố định P khi cát tuyến CAD thay đổi. b. Kẻ đường thẳng vuông góc với PA tại A, đường thẳng này cắt (O) tại E và cắt (O’) tại F. Chứng minh : \(AE = AF.\) c. Gọi AR, AQ lần lượt là đường kính của (O) và (O’). Chứng minh R, B, Q thẳng hàng. LG bài 1 Phương pháp giải: Sử dụng tính chất hai tiếp tuyến cắt nhau Lời giải chi tiết:
Ta có: \(AB + AC – BC \)\(\,= AM + MB + AS + SC – BN – NC\) Mà \(AM = AS, MB = NB, CS = NC\) (tính chất tiếp tuyến cắt nhau) \(⇒ AB + AC – BC \)\(\,= AM + AS = 2AM.\) LG bài 2 Phương pháp giải: a. Sử dụng định lý đường kính và dây cung và tính chất đường trung bình của hình thang b.Kẻ OM,ON' vuông góc với EF suy ra PA là đường trung bình của hình thang OMBO' c.Sử dụng tính chất góc nội tiếp chắn nửa đường tròn bằng 90 độ Lời giải chi tiết:
a. Ta có: H, K lần lượt là trung điểm của AC và AD (gt) nên OH ⊥ AC và O’K ⊥ AD (định lí đường kính dây cung). Do đó tứ giác OHKO’ là hình thang vuông. Gọi P là giao điểm của OO’ và đường thẳng qua I vuông góc với CD, ta có: IP là đường trung bình của hình thang OHKO’ \(⇒ P\) là trung điểm của OO’ nên P cố định. b. Kẻ OM, O’N lần lượt vuông góc với EF. Ta có OMBO’ là hình thang vuông có PA là đường trung bình nên A là trung điểm của MN hay \(AM = AN ⇒ AE = AF.\) c. Dễ thấy \(\widehat {ABR} = \widehat {ABQ} = 90^\circ \) (chắn các nửa đường tròn) \( \Rightarrow \widehat {RBA} + \widehat {ABQ} = 180^\circ \) \(⇒\) Ba điểm R, B, Q thẳng hàng. HocTot.Nam.Name.Vn
|