Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 1 - Hình học 6

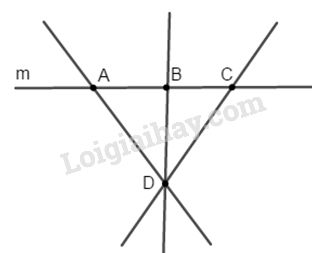
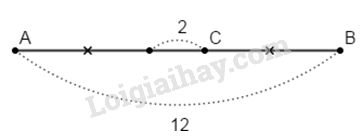
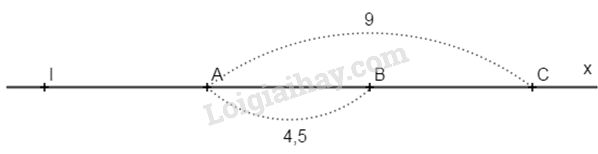
Đề bài

Bài 1. Vẽ đường thẳng m. Lấy A, B, C thuộc m và D không thuộc m. Kẻ các đường thẳng đi qua các cặp điểm.

a) Có bao nhiêu đường thẳng phân biệt? Viết tên các đường thẳng đó.

b) Những đường thẳng nào đồng quy (cùng cắt nhau) tại D?

Bài 2. Đoạn thẳng AB có độ dài 12cm; điểm C nằm giữa hai điểm A và B. Biết rằng CA - CB = 2cm. Tính độ dài các đoạn thẳng CA và CB.

Bài 3. Trên tia Ax lấy hai điểm B và C sao cho AB = 4,5cm, AC = 9cm.

a) Tính độ dài đoạn thẳng BC.

b) Chứng tỏ B là trung điểm của đoạn thẳng AC.

c) Trên tia đối của tia Ax lấy điểm I sao cho A là trung điểm của IB. Tính IC.

LG bài 1

Lời giải chi tiết:

a) Có 4 đường thẳng phân biệt đó là: m, AD, BD và CD.

b) Các đường thẳng cắt nhau tại D là DA, DB và DC.

LG bài 2

Phương pháp giải:

Nếu M nằm giữa hai điểm A và B thì: AM+MB=AB

Lời giải chi tiết:

 Ta có: \(CA+CB=AB=12cm\) (do C nằm giữa hai điểm A và B)

Lại có \(CA-CB=2cm\) 

Suy ra \(2CB = 12 – 2\)

\(2CB = 10\)

\(⇒ CB = 5 (cm)\)

Từ đó \(CA-CB=2\) hay \(CA-5=2\)

Suy ra \(CA=5+2=7cm\)

LG bài 3

Phương pháp giải:

Trên tia Ox, có OA<OB thì A nằm giữa O và B

Nếu M nằm giữa hai điểm A và B thì: AM+MB=AB

Nếu M là trung điểm của AB có: \(MA = MB = \frac{{AB}}{2}\)

Nếu MA và MB là hai tia đối nhau thì M nằm giữa hai điểm A và B

Nếu MA=MB và M nằm giữa A và B thì M là trung điểm của AB

Lời giải chi tiết:

a) Hai điểm B, C thuộc tia Ax mà \(AB < AC (4,5 < 9)\) nên B nằm giữa hai điểm A và C, ta có:

\( AB + BC = AC\)

\(4,5 + BC = 9\)

\(BC = 9-4,5 = 4,5 (cm)\)

b) B nằm giữa hai điểm A và C và \(AB = BC = 4,5 (cm)\). Do đó B là trung điểm của đoạn thẳng AC.

c) A là trung điểm của IB nên \(IA = AB = 4,5 (cm)\).

và AI và AB là hai tia đối nhau. Mặt khác AB, AC, Ax là các tia trùng nhau nên AI và AC là hai tia đối nhau. Do đó A nằm giữa hai điểm I và C.

Ta có: \(IA + AC = IC\) hay \(IC=AB+AC= 4,5 + 9 = 13,5 \;(cm).\)

HocTot.Nam.Name.Vn