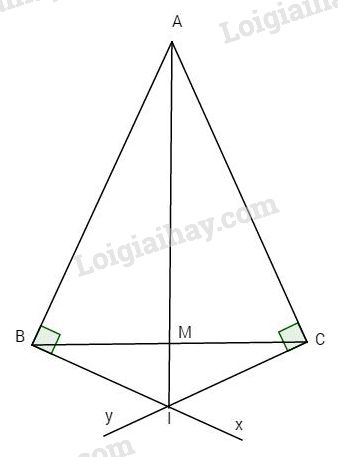
Đề kiểm tra 15 phút - Đề số 8 - Bài 7, 8 - Chương 2 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 7, 8 - Chương 2 - Hình học 7 Đề bài Cho tam giác ABC cân tại A. Kẻ qua B tia Bx vuông góc với AB, qua C kẻ tia Cy vuông góc với AC, gọi I là giao điểm của Bx và Cy. a) Chứng minh ΔABI=ΔACI. b) Chứng tỏ AI là đường trung trực của đoạn BC. Phương pháp giải - Xem chi tiết a. Hai tam giác bằng nhau theo trường hợp cạnh huyền-góc nhọn b.Gọi M là giao điểm của AI và BC Chứng minh MB=MC và AM vuông góc với BC Lời giải chi tiết
a) Ta có Bx⊥AB,Cy⊥AC. Xét hai tam giác vuông ABI và ACI có: +) AI cạnh chung, +) AB=AC (giả thiết). Do đó ΔABI=ΔACI (ch.cgv). b) ΔABI=ΔACI (chứng minh trên) ⇒^BAI=^CAI (góc tương ứng). Gọi M là giao điểm của AI và BC. Xét ΔAMB và ΔAMC có: +) AM cạnh chung; +) ^BAM=^CAM (chứng minh trên); +) AB=AC (giả thiết). Do đó ΔAMB=ΔAMC (c.g.c) ⇒MB=MC(1) và ^AMB=^AMC. Mà ^AMB+^AMC=180o (kề bù) ⇒^AMB=^AMC=90o. Chứng tỏ AM⊥BC (2). Từ (1) và (2) ⇒AI là đường trung trực của BC. HocTot.Nam.Name.Vn
|