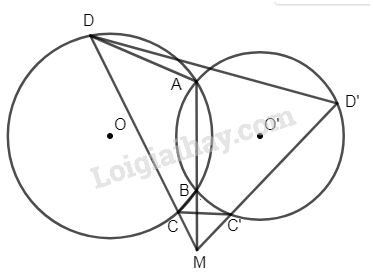
Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 3 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 3 - Hình học 9 Đề bài Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Gọi M là điểm tùy ý trên đường thẳng AB, nằm ngoài đoạn AB. Vẽ qua M hai cát tuyến MCD và MC’D’ với (O) và (O’). Chứng minh tứ giác CDD’C’ nội tiếp. Phương pháp giải - Xem chi tiết Sử dụng tam giác đồng dạng, chứng minh tứ giác CDD'C' có 1 góc trong bằng góc ngoài tại đỉnh đối diện Lời giải chi tiết
Ta có tứ giác ABCD nội tiếp trong đường tròn (O) nên \(\widehat {CDA} = \widehat {CBM}\) ( cùng bù với \(\widehat {ABC}\)). Do đó \(∆MBC\) đồng dạng \(∆MDA \) (g.g) \( \Rightarrow \dfrac{{MA}}{{MC}} =\dfrac {{MD} }{ {MB}}\) \( \Rightarrow MA.MB = MC.MD\) Chứng minh tương tự : \(MA.MB = MC’.MD’\) \( \Rightarrow MC.MD = MC’.MD’\) Do đó \(∆MCC’\) đồng dạng \(∆MD’D\) (g.g) \( \Rightarrow \widehat {MCC'} = \widehat {MD'D}\) Vậy tứ giác CDD’C’ nội tiếp. HocTot.Nam.Name.Vn
|