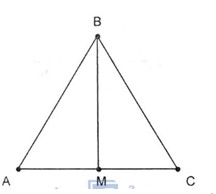
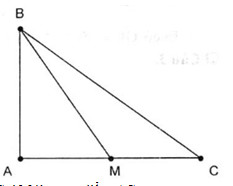
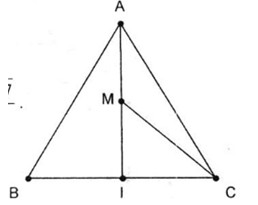
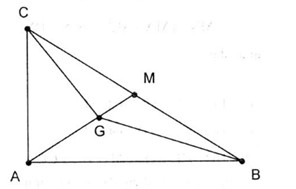
Đề kiểm tra 15 phút - Chương 1 - Đề số 4 - Hình học 10

Đề bài

Chọn phương án đúng

Câu 1. Cho tam giác đều ABC có cạnh bằng a. Độ dài của véctơ \(\overrightarrow {BA}  + \overrightarrow {BC} \) là

A.2a

B.\({{a\sqrt 3 } \over 2}\)

C.a

D.\(a\sqrt 3 \)

Câu 2. Cho tam giác ABC vuông tại A có AB=6, AC=8. Độ dài của véctơ \(\overrightarrow {BA}  + \overrightarrow {BC} \) là

A.\(2\sqrt 3 \)

B.10

C.\(4\sqrt {13} \)

D.16

Câu 3. Cho tam giác đều ABC có cạnh bằng 3. Gọi I là trung điểm của BC. Độ dài véctơ \(\overrightarrow {CA}  - \overrightarrow {IC} \) là

A.\(\dfrac{3 }{ 2}\)

B. \(\dfrac{3\sqrt 7 } {2}\)

C.\(2\sqrt 3 \)

D.\(\dfrac{9 }{ 2}\)

Câu 4. Cho tam giác ABC vuông tại A có BC = 15. Gọi G là trọng tâm. Độ dài của véctơ \(\overrightarrow {GB}  + \overrightarrow {GC} \) là

A.10                          B.5

C.15                          D.20

Câu 5. Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Tìm mệnh đề sai

A.\(\overrightarrow {AB}  + \overrightarrow {CD}  = 2\overrightarrow {MN} \)

B. \(\overrightarrow {AC}  + \overrightarrow {DB}  = 2\overrightarrow {MN} \)

C.\(\overrightarrow {AD}  + \overrightarrow {BC}  = 2\overrightarrow {MN} \) 

D. \(\overrightarrow {CA}  - \overrightarrow {BD}  = 2\overrightarrow {NM} \)

Câu 6. Cho lục giác ABCDEF. Tìm mệnh đề đúng

A.\(\overrightarrow {AD}  + \overrightarrow {BE}  + \overrightarrow {CF}  = \overrightarrow {AF}  + \overrightarrow {BD}  + \overrightarrow {CD} \)

B.\(\overrightarrow {AD}  + \overrightarrow {BE}  + \overrightarrow {CF}  = \overrightarrow {AE}  + \overrightarrow {BF}  + \overrightarrow {CE} \)

C.\(\overrightarrow {AD}  + \overrightarrow {BE}  + \overrightarrow {CF}  = \overrightarrow {AD}  + \overrightarrow {BF}  + \overrightarrow {CF} \)

D.\(\overrightarrow {AD}  + \overrightarrow {BE}  + \overrightarrow {CF}  = \overrightarrow {AF}  + \overrightarrow {BD}  + \overrightarrow {CE} \)

Câu 7. Cho tam giác OAB. Gọi M, N lần lượt là trung điểm OA, OB . Tìm mệnh đề đúng

A.\(\overrightarrow {MN}  = \dfrac{1 }{ 2}\overrightarrow {OA}  + \dfrac{1 }{ 2}\overrightarrow {OB} \)

B. \(\overrightarrow {MN}  = \dfrac{1}{2}\overrightarrow {OB}  - \dfrac{1 }{ 2}\overrightarrow {OA} \)

C. \(\overrightarrow {MN}  = \dfrac{1}{2}\overrightarrow {OA}  - \dfrac{1 }{2}\overrightarrow {OB} \)   

D.\(\overrightarrow {MN}  = \overrightarrow {OA}  + \overrightarrow {OB} \)

Câu 8. Cho  hình bình hành ABCD. Gọi G là trọng tâm tam giác ABC. Tìm mệnh đề sai

A.\(\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = 3\overrightarrow {DG} \)

B.\(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GD}  = \overrightarrow {CD} \)

C.\(\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = \overrightarrow {DG} \)          

D.\(\overrightarrow {GA}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow {BD} \)

Câu 9. Cho hình bình hành ABCD và \(AB'C'D'\) có chung đỉnh A. Tìm mệnh đề đúng

A.\(BCC'B'\) là hình bình hành

B.\(\overrightarrow {CC'}  = \overrightarrow {BB'}  + \overrightarrow {DD'} \)

C.\(C{\rm{DD}}'C'\) là hình bình hành

D.\(\overrightarrow {AC}  = \overrightarrow {AC'} \)

Câu 10. Tam giác ABC là tam giác gì nếu thỏa mãn điều kiện \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right|\) ?

A.Vuông                 B. Cân

C. Đều                   D. Nhọn

Lời giải chi tiết

Câu 1.D

Gọi M là trung điểm AC. Khi đó \(\overrightarrow {BA}  + \overrightarrow {BC}  = 2\overrightarrow {BM} \) .

 Mà \(BM = \dfrac{a\sqrt 3 } { 2}\) . Do đó \(\left| {\overrightarrow {BA}  + \overrightarrow {BC} } \right| = \left| {2\overrightarrow {BM} } \right| = 2BM = a\sqrt 3 \) .

Câu 2.C

Gọi M là trung điểm AC.

Khi đó \(\overrightarrow {BA}  + \overrightarrow {BC}  \)\(\,= 2\overrightarrow {BM} \) .

Mà \(BM = \sqrt {A{B^2} + A{M^2}}  = \sqrt {36 + 16}  \)\(\,= 2\sqrt {13} \) .

Do đó \(\left| {\overrightarrow {BA}  + \overrightarrow {BC} } \right| = \left| {2\overrightarrow {BM} } \right| = 2BM \)\(\,= 4\sqrt {13} \) .

Câu 3.B

Gọi M là trung điểm AI.

Theo Pitago ta có:

\(AI = \sqrt {A{C^2} - I{C^2}} \)\( = \sqrt {{3^2} - {{\left( {\frac{3}{2}} \right)}^2}}  = \frac{{3\sqrt 3 }}{2} \)

\(\Rightarrow MI = \frac{1}{2}AI = \frac{{3\sqrt 3 }}{4}\)

Khi đó \(\overrightarrow {CA}  - \overrightarrow {IC}  = \overrightarrow {CA}  + \overrightarrow {CI}  = 2\overrightarrow {CM} \) .

Mà \(CM = \sqrt {C{I^2} + M{I^2}}  \)\(\; = \sqrt {{{\left( {\dfrac{3}{2}} \right)}^2} + {{\left( {\dfrac{{3\sqrt 3 }}{4}} \right)}^2}}  = \dfrac{{3\sqrt 7 }}{4}\).

Vậy \(\left| {\overrightarrow {CA}  - \overrightarrow {IC} } \right| = \left| {2\overrightarrow {CM} } \right| = 2CM = \dfrac{3\sqrt 7 }{ 2}\) .

Câu 4.B

Gọi M là trung điểm BC.

Ta có \(\overrightarrow {GB}  + \overrightarrow {GC}  = 2\overrightarrow {GM} \) .

Mà \(GM = \dfrac{1}{3}AM = \dfrac{1}{6}BC = \dfrac{{15}}{6} = \dfrac{5}{2}\).

Do đó \(\left| {\overrightarrow {GB}  + \overrightarrow {GC} } \right| = \left| {2\overrightarrow {GM} } \right| = 2GM = 5\) .

Câu 5.A

Ta có

\(\overrightarrow {AC}  + \overrightarrow {BD}  \)

\(= \overrightarrow {AM}  + \overrightarrow {MN}  + \overrightarrow {NC}  + \overrightarrow {BM}  + \overrightarrow {MN}  + \overrightarrow {ND} \)

\(= 2\overrightarrow {MN}  + \left( {\overrightarrow {AM}  + \overrightarrow {BM} } \right) + \left( {\overrightarrow {NC}  + \overrightarrow {ND} } \right) \)

\(= 2\overrightarrow {MN} \) 

Suy ra (B) là mệnh đề đúng.

Tương tự

\(\overrightarrow {AD}  + \overrightarrow {BC} \)

\(= \overrightarrow {AM}  + \overrightarrow {MN}  + \overrightarrow {ND}  + \overrightarrow {BM}  + \overrightarrow {MN}  + \overrightarrow {NC} \)

\( = 2\overrightarrow {MN}  + \left( {\overrightarrow {AM}  + \overrightarrow {BM} } \right) + \left( {\overrightarrow {NC}  + \overrightarrow {ND} } \right)\)

\(= 2\overrightarrow {MN} \)

Vậy (C) là mệnh đề đúng.

Cũng vậy:

\(\overrightarrow {CA}  - \overrightarrow {BD} \)\(\,= \overrightarrow {CN}  + \overrightarrow {MN}  + \overrightarrow {MA}  - \left( {\overrightarrow {BM}  + \overrightarrow {MN}  + \overrightarrow {ND} } \right)\)

\( = 2\overrightarrow {MN}  + \left( {\overrightarrow {MA}  + \overrightarrow {MB} } \right) + \left( {\overrightarrow {CN}  + \overrightarrow {DN} } \right)\)\( = 2\overrightarrow {MN} \)

Do đó (D) là mệnh đề đúng.

Câu 6.D

\(\overrightarrow {AD}  + \overrightarrow {BE}  + \overrightarrow {CF}  \)

\(= \overrightarrow {AF}  + \overrightarrow {FD}  + \overrightarrow {BD}  + \overrightarrow {DE}  + \overrightarrow {CE}  + \overrightarrow {EF} \)

\( = \overrightarrow {AF}  + \overrightarrow {BD}  + \overrightarrow {CE}  + \overrightarrow {FD}  + \overrightarrow {DE}  + \overrightarrow {EF} \)

Chú ý kết quả đúng khi thứ tự các điểm đầu được giữ nguyên, chỉ hoán vị vòng quanh các điểm cuối.

Câu 7.B

Ta có \(\overrightarrow {MN}  = \overrightarrow {ON}  - \overrightarrow {OM}  = {1 \over 2}\overrightarrow {OB}  - {1 \over 2}\overrightarrow {OA} \) .

Vậy (B) đúng.

Câu 8.C

Hiển nhiên \(\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = 3\overrightarrow {DG} \) .

Mặt khác

\(\eqalign{  & \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GD}  \cr&= \overrightarrow {GA}  + \overrightarrow {GB}  - 2\overrightarrow {GB}   \cr  & {\rm{                        }} = \overrightarrow {GA}  - \overrightarrow {GB}  = \overrightarrow {BA}  = \overrightarrow {CD}  \cr} \) .

Tương tự \(\overrightarrow {GA}  + \overrightarrow {GC}  + \overrightarrow {GD}  = 2\overrightarrow {GO}  + \overrightarrow {GD}  \)\(\,= \overrightarrow {GD}  - \overrightarrow {GB}  = \overrightarrow {BD} \) .

Vậy (A), (B), (D) là các mệnh đề đúng

Câu 9.B

Ta có:

\(\overrightarrow {BB'}  + \overrightarrow {DD'} \)

\(\;= \overrightarrow {AB'}  - \overrightarrow {AB}  + \overrightarrow {AD'}  - \overrightarrow {AD} \)

\(\eqalign{  &  = \left( {\overrightarrow {AB'}  + \overrightarrow {AD'} } \right) - \left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right)  \cr  &  = \overrightarrow {AC'}  - \overrightarrow {AC}  = \overrightarrow {CC'}  \cr} \) .

Câu 10.A

Vẽ hình bình hành ABDC.

Ta có \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} ,{\rm{ }}\overrightarrow {AB}  - \overrightarrow {AC}  = \overrightarrow {CB} \) .

Do đó \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right| \)\(\,\Leftrightarrow AD = CB \Leftrightarrow ABDC\) là hình chữ nhật.

Vậy ABC là tam giác vuông tại A.

 HocTot.Nam.Name.Vn