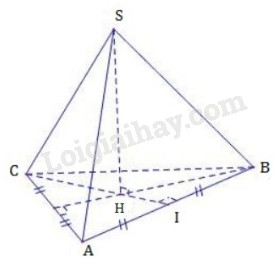
Đề kiểm tra 15 phút - Đề số 4 - Chương I - Hình học 12Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Đề số 4 - Chương I - Hình học 12 Đề bài Câu 1: Số cạnh của hình mười hai mặt đều là: A. 30 B. 16 C. 20 D. 12 Câu 2: Số cạnh của một hình bát diện đều là: A. 10 B. 16 C. 8 D. 12 Câu 3: Số đỉnh của một hình bát điện đều là: A. 10 B. 12 C. 8 D. 6 Câu 4: Số đỉnh của hình hai mươi mặt đều là: A. 40 B. 20 C. 16 D. 12 Câu 5: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Hình chiếu vuông góc của tam giác SAB xuống mặt phẳng (ABC) có diện tích bằng: \(A.\,\,\dfrac{{{a^2}\sqrt 3 }}{{16}}\) \(B.\,\,\dfrac{{{a^2}\sqrt 3 }}{9}\) \(C.\,\,\dfrac{{{a^2}\sqrt 3 }}{{12}}\) \(D.\,\,\dfrac{{{a^2}\sqrt 3 }}{6}\) Câu 6: Số đỉnh của một hình mười hai mặt đều là: A. 12 B. 30 C. 16 D. 20 Câu 7: Trong các mệnh đề sau, mệnh đề nào sai? A. Hình lập phương là đa diện lồi. B. Hình hộp là đa diện lồi. C. Hình tạo bởi hai tứ diện đều ghép với nhau là một hình đa diện lồi. D. Tứ diện là đa diện lồi. Câu 8: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi I là trung điểm của cạnh SC. Hình chiếu vuông góc của tam giác IAB xuống mặt phẳng (ABC) có diện tích bằng: \(A.\,\dfrac{{{a^2}\sqrt 3 }}{{18}}\) \(B.\,\,\dfrac{{3{a^2} }}{{8}}\) \(C.\,\,\dfrac{{{a^2}\sqrt 3 }}{9}\) \(D.\,\,\dfrac{{{a^2}\sqrt 3 }}{6}\) Câu 9: Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau: A. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt B. Mỗi cạnh là cạnh chung của ít nhất ba mặt. C. Mỗi mặt có ít nhất ba cạnh D. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh Lời giải chi tiết
Câu 1 Đáp án A. Câu 2 Đáp án D. Câu 3 Đáp án D. Câu 4 Đáp án D. Câu 5
Gọi H là giao điểm của các đường cao trong tam giác ABC Vì tam giác ABC đều nên \(AB = AC = BC = a\) Hình chiếu vuông góc của tam giác SAB xuống mặt phẳng (ABC) là tam giác HAB Đường cao của tam giác HAB là \(h = \dfrac{1}{3}\sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{6}\) Khi đó \({S_{HAB}} = \dfrac{1}{2}.h.AB = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{6}.a\)\(\, = \dfrac{{{a^2}\sqrt 3 }}{{12}}\) Chọn đáp án C. Câu 6 Đáp án D. Câu 7 Đáp án C. Câu 8 Áp dụng như bài câu 5 Diện tích cần tìm là \(2.\dfrac{{{a^2}\sqrt 3 }}{{24}} = \dfrac{{{a^2}\sqrt 3 }}{{12}}\) Chọn đáp án B Câu 9 Đáp án B. HocTot.Nam.Name.Vn
|