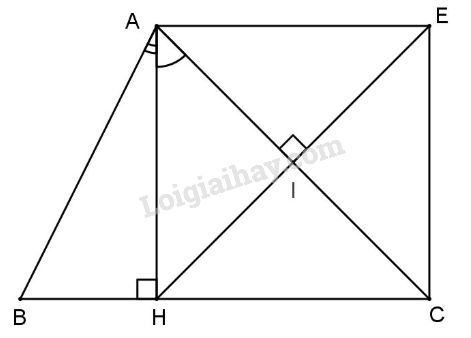
Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 3 – Hình học 7 Đề bài Cho tam giác ABC có \(AB < AC\), kẻ \(AH \bot BC\) (H thuộc BC); \(HI \bot AC\) (I thuộc AC). Trên tia đối của tia IH lấy điểm E sao cho \(IE = HI\). a) Chứng minh \(A{\rm{E}} \bot CE;\) b) Chứng minh \(\widehat {BAH} < \widehat {CAH}\). Phương pháp giải - Xem chi tiết Sử dụng: Tam giác bằng nhau Tổng ba góc của 1 tam giác bằng 90 độ Lời giải chi tiết
a) Vì \(HI = EI\) (gt) và \(HI \bot AC\) (gt) nên \(\Delta AIH = \Delta AI{\rm{E}}\) (c.g.c) \( \Rightarrow A{\rm{E}} = AH\). Tương tự ta có \(\Delta CIH = \Delta CIE\) \(\Rightarrow CE = CH\). Xét \(\Delta A{\rm{E}}C\) và \(\Delta AHC\) có: +) AC cạnh chung +) \(A{\rm{E}} = AH\) +) \(CE = CH\) (cmt). Do đó \( \Rightarrow \Delta A{\rm{E}}C = \Delta AHC\) (c.c.c) \( \Rightarrow \widehat {A{\rm{E}}C} = \widehat {AHC} = {90^0}\) hay \(A{\rm{E}} \bot {\rm{CE}}.\) b) Ta có \(\widehat {BAH} + \widehat B = {90^0}\) (1) (Vì \(\widehat {AHB} = {90^0}\)); \(\widehat {CAH} + \widehat C = {90^0}\) (2) (Vì \(\widehat {AHC} = {90^0}\)); Mà \(AB < AC\) (gt) \( \Rightarrow \widehat C < \widehat B\) (3) Từ (1), (2), (3) \( \Rightarrow \widehat {BAH} < \widehat {CAH}\). HocTot.Nam.Name.Vn
|