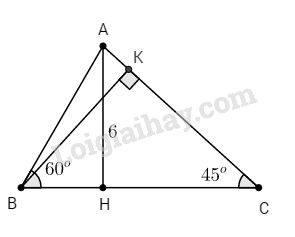
Đề kiểm tra 15 phút - Đề số 3 - Bài 4 - Chương 1 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 4 - Chương 1 - Hình học 9 Đề bài Cho ∆ABC nhọn. a. Chứng minh rằng : \(\sin A + \cos A > 1\) b. Kẻ đường cao AH của tam giác ABC. Biết \(\widehat B = 60^\circ ,\,\widehat C = 45^\circ ,\) đường cao \(AH = 6cm\). Tính \({S_{ABC}}\) Phương pháp giải - Xem chi tiết Sử dụng: Tam giác ABC có \(AB+AC>BC\) Định nghĩa tỉ số lượng giác của góc nhọn Trong một tam giác vuông, mỗi cạnh góc vuông bằng: Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề. Diện tích tam giác bằng nửa tích cạnh huyền và chiều cao tương ứng. Lời giải chi tiết
a. Kẻ đường cao BK, khi đó ∆AKB vuông tại K. \(\eqalign{ & \sin A = {{BK} \over {AB}};\,\cos A = {{AK} \over {AB}} \cr & \Rightarrow \sin A + \cos A = {{BK + AK} \over {AB}} >\frac{{AB}}{{AB}} = 1 \cr} \) (bất đẳng thức tam giác) b. Ta có: ∆AHC vuông cân(tam giác vuông có \(\widehat C = 45^\circ \))nên \(HC = AH = 6\;(cm)\) \(∆AHB\) vuông tại H có \(\widehat B = 60^\circ \) nên: \(BH = AH.\cot 60^\circ = 6.\cot 60^\circ \)\(\,= 2\sqrt 3 \,\left( {cm} \right)\) Do đó: \(BC = BH + HC = 2\sqrt 3 + 6 \)\(\,= 2\left( {\sqrt 3 + 3} \right)\,\left( {cm} \right)\) Vậy : \({S_{ABC}} = {1 \over 2}BC.AH \)\(\,= {1 \over 2}.2\left( {\sqrt 3 + 3} \right).6 \)\(\,= 6\left( {\sqrt 3 + 3} \right)\,\left( {c{m^2}} \right)\) HocTot.Nam.Name.Vn
|