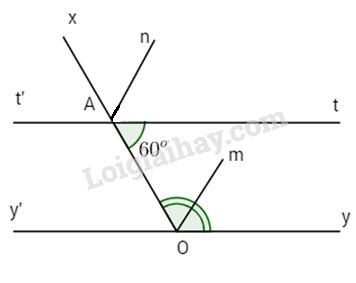
Đề kiểm tra 15 phút - Đề số 3 - Bài 3, 4 - Chương 1 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 3, 4 - Chương 1 - Hình học 7 Đề bài Cho góc \(\widehat {xOy} = {120^o}\). Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng chứa tia Oy bờ là Ox, vẽ tia At sao cho \(\widehat {OAt} = {60^o}\). Gọ At’ là tia đối của tia At. a) Chứng tỏ tt’ // Oy. b) Gọi Om, An theo thứ tự là các tia phân giác của các góc \(\widehat {xOy}\) và \(\widehat {xAt}\). Chứng tỏ Om//An. Phương pháp giải - Xem chi tiết Sử dụng: Hai góc kề bù có tổng bằng \(180^0\) Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì \(a\) và \(b\) song song với nhau. Lời giải chi tiết
a) Kẻ Oy’ là tia đối của tia Oy, ta có \(\widehat {xAn} = \widehat {xOm} = {60^o}\) \(\widehat {xOy} + \widehat {xOy'} = {180^o}\) (kề bù) \( \Rightarrow \widehat {xOy'} = {180^o} - \widehat {xOy'}\) \( \Rightarrow \widehat {xOy'} = {180^o} - {120^o} = {60^o}.\) \( \Rightarrow \widehat {xOy'} = \widehat {OAt} = {60^o}\). Hai góc này ở vị trí so le trong. Do đó tt’ // Oy. b) Ta có \(\widehat {xAt} + \widehat {OAt} = {180^o}\)(kề bù) \( \Rightarrow \widehat {xAt} = {180^o} - \widehat {OAt} \)\(\,= {180^o} - {60^o} = {120^o},\) Lại có An là tia phân giác của \(\widehat {xAt}\) nên \(\widehat {xAn} = \widehat {tAn} = \dfrac{1 }{2}\widehat {xAt} = \dfrac{1 }{2}{.120^o} = {60^o}.\) Tương tự Om là phân giác của \(\widehat {xOy}\) nên \(\widehat {xOm} = \widehat {yOm} = \dfrac{1 }{ 2}\widehat {xOy} \)\(\,= \dfrac{1}{ 2}{.120^o} = {60^o}.\) Khi đó \(\widehat {xAn} = \widehat {xOm} = {60^o}\). Hai góc này ở vị trí đồng vị. Do đó Om // An. HocTot.Nam.Name.Vn
|