Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 3 - Đại số 9Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 3 - Đại số 9
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Bài 1: Cho phương trình : \(\left( {m - 1} \right)x + \left( {m + 1} \right)y = 1.\) a) Tìm m để cặp số (1; 1) là một nghiệm của phương trình. b) Cặp số \(\left( { - {1 \over 2};{1 \over 2}} \right)\) có phải là nghiệm của phương trình hay không ? Bài 2: Cho phương trình \(3x – 2y = 2.\) a) Viết công thức nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của phương trình. b) Tìm các nghiệm nguyên của phương trình. LG bài 1 Phương pháp giải: a.Thế x,y vào vào phương trình từ đó tìm m b. Thế x,y vào phương trình ta chứng minh 2 vế của phương trình bằng nhau Lời giải chi tiết: a) Thế \(x = 1; y = 1\) vào phương trình, ta được : \(m - 1 + m + 1 = 1 \Leftrightarrow m = {1 \over 2}\) b)Thế \(x = - {1 \over 2};y = {1 \over 2}\) vào phương trình, ta được : \( - {1 \over 2}\left( {m - 1} \right) + {1 \over 2}\left( {m + 1} \right) = 1\) \( \Leftrightarrow - {1 \over 2}m + {1 \over 2} + {1 \over {2m}} + {1 \over 2} = 1\)( luôn đúng với mọi m) Vậy cặp số \(\left( { - {1 \over 2};{1 \over 2}} \right)\) là nghiệm của phương trình. Nhận xét : Điểm \(\left( { - {1 \over 2};{1 \over 2}} \right)\) là điểm cố định mà họ đường thẳng \(\left( {m - 1} \right)x + \left( {m + 1} \right)y = 1\) luôn đi qua khi m thay đổi. LG bài 2 Phương pháp giải: a.Rút y từ phương trình từ đó suy ra công thức nghiệm tổng quát, lập bảng giá trị từ đó biểu diễn tập nghiệm trên hệ trục tọa độ Oxy b.Rút y từ phương trình và ta tìm x,y tổng quát sao cho x,y nguyên Lời giải chi tiết: Bài 2: a) Ta có : \(3x – 2y = 2 \)\( \Leftrightarrow y = {3 \over 2}x - 1\) Công thức nghiệm tổng quát : Vẽ đường thẳng \(y = {3 \over 2}x - 1\) : Bảng giá trị :
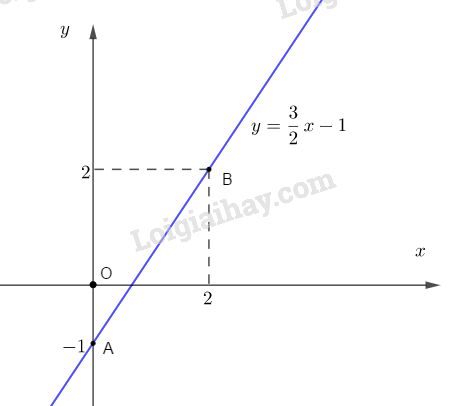
Đường thẳng qua hai điểm : \((0; −1)\) và \(( 2; 2).\)
b) Ta có : \(3x - 2y = 2 \Leftrightarrow y = {3 \over 2}x - 1\) \(\Leftrightarrow y = x - 1 + {x \over 2}\) Ta tìm sao cho ( khi đó ); Khi đó nghiệm nguyên là cặp số \((2k; 3k – 1)\) HocTot.Nam.Name.Vn
|