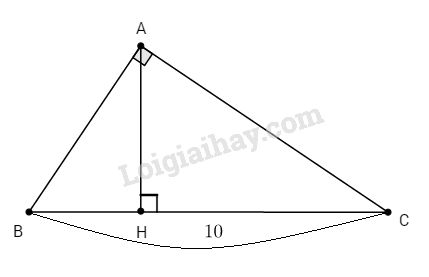
Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 9 Đề bài Cạnh huyền của một tam giác vuông là 10cm, các cạnh góc vuông tỉ lệ với 4 và 3. Tính độ dài hình chiếu của mỗi cạnh góc vuông lên cạnh huyền. Phương pháp giải - Xem chi tiết Sử dụng: Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), ta có: \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\) Tính chất của dãy tỉ số bằng nhau: \(\dfrac {a}{b}=\dfrac {c}d=\dfrac{a+c}{b+d}\) Lời giải chi tiết
Tam giác ABC vuông tại A, chiều cao AH có \(AB=c;AC=b;BC=a=10cm\) Theo bài ra, ta có: \({b \over c} = {4 \over 3} \Rightarrow {b \over 4} = {c \over 3}\) \(\eqalign{ & \Rightarrow {{{b^2}} \over {16}} = {{{c^2}} \over 9} = {{{b^2} + {c^2}} \over {16 + 9}} = {{{a^2}} \over {25}} \cr&\;\;\;\;\;\;\;\;\;\;\;= {{{{10}^2}} \over {25}} = 4 \cr & \Rightarrow {b^2} = 4.16 \Rightarrow b = 8\,\left( {cm} \right) \cr} \) Và \(c^2=9.4=36\) suy ra \(c = 6cm\) \(∆ABC\) vuông tại A, đường cao AH. Ta có: \({b^2} = a.b'\) (định lí 1) \( \Rightarrow b' = {{{b^2}} \over a} = {{{8^2}} \over {10}} = 6,4\,\left( {cm} \right)\) Do đó: \(c' = a - b' = 10 - 6,4 = 3,6\,\left( {cm} \right)\) Cách khác: Đặt \(b = 4k, c = 3k\) (vì \({b \over 4} = {c \over 3} = k\)), ta có: \(\eqalign{ & {\left( {4k} \right)^2} + {\left( {3k} \right)^2} = {10^2} \cr&\Leftrightarrow 16{k^2} + 9{k^2} = 100 \cr & \Leftrightarrow 25{k^2} = 100\cr& \Leftrightarrow {k^2} = 4 \Leftrightarrow k = 2 \cr} \) Do đó: \(b = 4.2 = 8\; (cm)\) và \(c = 3.2 = 6\; (cm)\). HocTot.Nam.Name.Vn
|