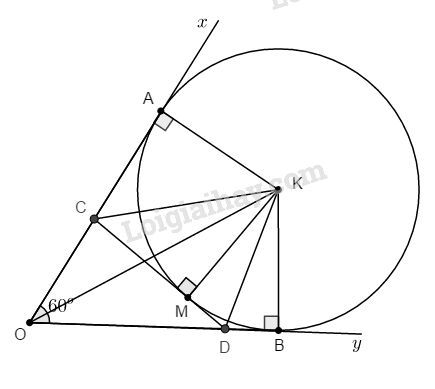
Đề kiểm tra 15 phút - Đề số 2 - Bài 6 - Chương 2 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 6 - Chương 2 - Hình học 9 Đề bài Cho góc \(\widehat {xOy} = 60^\circ .\) Đường tròn tâm K bán kính R tiếp xúc với Ox tại A và Oy tại B. Từ điểm M trên cung nhỏ AB, vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt Ox, Oy lần lượt tại C và D. a. Tính chu vi ∆COD theo R. Chứng tỏ chu vi đó không đổi khi M chạy trên cung nhỏ AB. b. Chứng minh số đo \(\widehat {CKD}\) không đổi khi M chạy trên cung nhỏ AB. Phương pháp giải - Xem chi tiết a.Sử dụng: +Tính chất hai tiếp tuyến cắt nhau +Tính chất nửa tam giác đều b.Chứng minh CD,DK lần lượt là phân giác của các góc AKM và BKM từ đó suy ra góc CKD bằng nửa góc AKB Lời giải chi tiết
a. Ta có: OA, OB là hai tiếp tuyến của (O) nên \(OA = OB\) và OK là phân giác của\(\widehat {AOB} \Rightarrow \widehat {AOK} = \widehat {BOK} = {{\widehat {AOB}} \over 2}\)\(\; = {{60^\circ } \over 2} = 30^\circ \) Do đó ∆OAK là nửa tam giác đều có cạnh \(AK = R ⇒ OK = 2R\) nên \(OA = OB = \sqrt {O{K^2} - A{K^2}} \)\(\;= \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = R\sqrt 3 \) Lại có CD tiếp xúc với (K) tại M nên \(CM = CA\) và \(DM = DB.\) Gọi p là chu vi của ∆OCD, ta có: \(p = OC + CM + MD + OD\) \(\;\;\;= OC + CA + DB + OD\) \(\;\;\;=2OA = 2R\sqrt 3 \) (không đổi) b. Ta có: CK là phân giác của \(\widehat {AKM},\) DK là phân giác của \(\widehat {BKM}\) mà \(\widehat {AKM} + \widehat {BKM} = \widehat {AKB} = 120^\circ \) (vì \(\widehat O = 60^\circ \,và\,\widehat A = \widehat B = 90^\circ \) ) \( \Rightarrow \widehat {CKD} = {1 \over 2}\widehat {AKB} = {1 \over 2}.120^\circ = 60^\circ \) (không đổi) HocTot.Nam.Name.Vn
|