Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Đại số 9Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Đại số 9
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Bài 1. Tìm tập xác định của mỗi hàm số: a. \(y = {1 \over {\sqrt {x + 2} }}\) b. \(y = {1 \over x}\) Bài 2. Cho hàm số \(y = f\left( x \right) = \sqrt {1 - x} .\) Tính : \(f\left( { - 1} \right);\,f\left( { - 3} \right);\,f\left( 3 \right)\) Bài 3. Vẽ đồ thị hàm số \(y=-x\) LG bài 1 Phương pháp giải: Sử dụng \(\sqrt A \) xác định khi \(A\ge 0\) \(\dfrac{1}{B}\) xác định khi \(B\ne 0\) Lời giải chi tiết: a. Hàm số \(y={1 \over {\sqrt {x + 2} }}\) xác định \( \Leftrightarrow \left\{ {\matrix{ {x + 2 \ge 0} \cr {x + 2 \ne 0} \cr } } \right. \) \(\Leftrightarrow x + 2 > 0 \Leftrightarrow x > - 2\) b. Hàm số \(y={1 \over x}\) xác định \( \Leftrightarrow x \ne 0\) LG bài 2 Phương pháp giải: Để tính giá trị \({y_0}\) của hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\) ta thay \(x = {x_0}\) vào \(f\left( x \right)\), ta được \({y_0} = f\left( {{x_0}} \right)\). Lời giải chi tiết: Vì \(\sqrt {1 - x} \) xác định \( \Leftrightarrow 1 - x \ge 0 \Leftrightarrow x \le 1\) Vậy \(f(3)\) không tồn tại (do \(x=3\) không thỏa mãn điều kiện xác định) Ta có: \(\eqalign{ & f\left( { - 1} \right) = \sqrt {1 - \left( { - 1} \right)} = \sqrt 2 \cr & f\left( { - 3} \right) = \sqrt {1 - \left( { - 3} \right)} = \sqrt 4 = 2 \cr} \) LG bài 3 Phương pháp giải: Cách vẽ đồ thị của hàm số \(y = ax + b (a ≠ 0).\) - Chọn điểm \(P(0; b)\) (trên trục \(Oy\)). - Chọn điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) (trên trục \(Ox\)). - Kẻ đường thẳng \(PQ\) ta được đồ thị của hàm số \(y=ax+b.\) Lời giải chi tiết: Bảng giá trị :
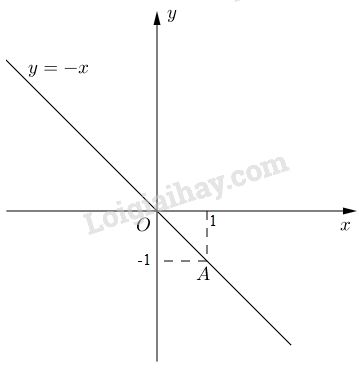
Đồ thị của hàm số \(y = -x\) là đường thẳng qua hai điểm \(O(0; 0)\) và \(A(1; -1)\).
HocTot.Nam.Name.Vn
|