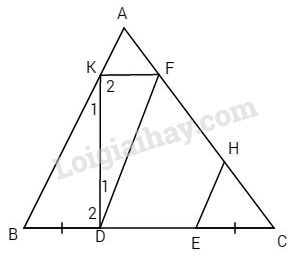
Đề kiểm tra 15 phút - Đề số 13 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7

Đề bài

Cho tam giác ABC. Trên cạnh BC lấy hai điểm D và E sao cho D nằm giữa B và E và BD = CE. Qua D và E vẽ DF và EH song song với AB. (F và H thuộc AC).

Chứng minh rằng: AB = DF + EH.

Lời giải chi tiết

Kẻ FK // BC, nối K với D. Ta có $\Rightarrow AB = DF + EH.$ $\widehat {{K_2}} = \widehat {{D_1}}$ (1) (cặp góc so le trong).

Lại có DF //AB (giả thiết) $\Rightarrow \widehat {{K_1}} = \widehat {{D_1}}$ (2)

Xét $\Delta KBD$ và $\Delta DFK$ có (1), (2) và KD cạnh chung.

Do đó $\Delta KBD=\Delta DFK$ (g.c.g).

$\Rightarrow BK = DF$ (3) và $BD= KF$ (cạnh tương ứng),

Mà $BD = CE$ (giả thiết) $\Rightarrow KF = CE$  (4).

Mặt khác KF // BC $\Rightarrow \widehat {AFK} = \widehat {ACB}$ (5) (cặp góc đồng vị).

Tương tự $\widehat {AFK} = \widehat {ABC}$.

Lại có HE // AB (giả thiết) $\Rightarrow \widehat {ABC} = \widehat {HEC}$ (6)

$\Rightarrow \widehat {AKF} = \widehat {HEC}$ (6)

Từ (4), (5) và (6) ta có $\Delta AKF = \Delta HEC$ (g.c.g) $\Rightarrow AK = HE$ (7)

Vì $AB = BK + AK$. Từ (3) và (7) $\Rightarrow AB = DF + EH.$

HocTot.Nam.Name.Vn