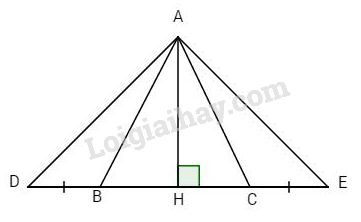
Đề kiểm tra 15 phút - Đề số 10 - Bài 7, 8 - Chương 2 - Hình học 7

Đề bài

Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC. 

a) Chứng minh $\Delta AHB = \Delta AHC$

b) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia Cb lấy điểm E sao cho $BD = CE$. Chứng minh rằng $\Delta ADE$ cân.

Lời giải chi tiết

a) $AH \bot BC$ (giả thiết).

Xét hai tam giác vuông AHB và AHC có :

+) AH cạnh chung,

+) $AB = AC$ (giả thiết).

Do đó $\Delta AHB = \Delta AHC$ (ch.cgv).

b) Ta có $\widehat {ABD} + \widehat {ABC} = {180^o}$ (kề bù),

Tương tự $\widehat {ACE} + \widehat {ACB} = {180^o}$ mà $\widehat {ABC} = \widehat {ACB}$ (giả thiết)

$\Rightarrow \widehat {ABD} = \widehat {ACE}$  (1).

Xét $\Delta ABD$ và $\Delta ACE$ có:

+) $AB = AC$ (giả thiết) 

+) $\widehat {ABD} = \widehat {ACE}$ 

+) $DB = CE$ (giả thiết).

Do đó $\Delta ABD = \Delta ACE$ (c.g.c)

$\Rightarrow AD = AE$ hay $\Delta ADE$ cân.

HocTot.Nam.Name.Vn