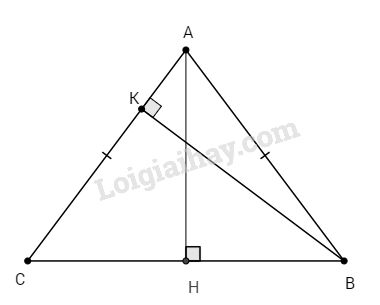
Đề kiểm tra 15 phút - Đề số 10 - Bài 1 - Chương 1 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 10 - Bài 1 - Chương 1 - Hình học 9 Đề bài Cho \(∆ ABC\) cân tại A. Vẽ các đường cao AH, BK. Chứng minh rằng: \({1 \over {B{K^2}}} = {1 \over {B{C^2}}} + {1 \over {4A{H^2}}}\) Phương pháp giải - Xem chi tiết Sử dụng hệ thức lượng trong tam giác vuông Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Ta có: \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\) Lời giải chi tiết
Ta có: ∆ABC cân tại A, đường cao AH đồng thời là đường trung tuyến \( \Rightarrow HB = HC = {{BC} \over 2}\) (1) Kẻ \(HI ⊥ AC\), ta có HI là đường trung bình của ∆BKC \( \Rightarrow HI = {{BK} \over 2}\) (2) Lại có: ∆AHC vuông có đường cao HI. \( \Rightarrow {1 \over {H{I^2}}} = {1 \over {H{C^2}}} + {1 \over {A{H^2}}}\) (3) (định lí 4) Thay (1), (2) vào (3), ta có: \({1 \over {{{\left( {{{BK} \over 2}} \right)}^2}}} = {1 \over {{{\left( {{{BC} \over 2}} \right)}^2}}} + {1 \over {A{H^2}}}\) \(\Rightarrow {1 \over {B{K^2}}} = {1 \over {B{C^2}}} + {1 \over {4A{H^2}}}\) (đpcm) HocTot.Nam.Name.Vn
|