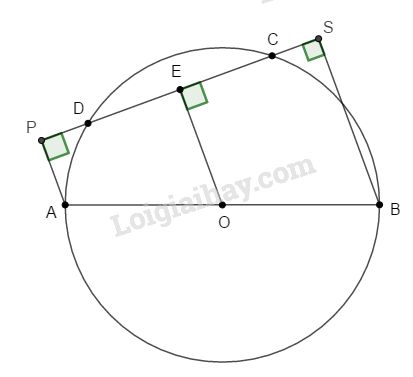
Đề kiểm tra 15 phút - Đề số 1 - Bài 4 - Chương 2 - Hình học 9

Đề bài

Cho nửa đường tròn (O), đường kính AB và một dây cung CD. Vẽ AP và BS vuông góc với CD. Chứng minh:

a. P và S ở bên ngoài đường tròn.

b. \(PC = DS\)

Lời giải chi tiết

a. Ta có: AP // BS (⊥ CD) nên tứ giác APSB là hình thang vuông.

Kẻ \(OE ⊥ CD.\) Khi đó OE là đường trung bình của hình thang nên \(EP = ES.\)

Trong hình thang APSD có: 

\(\widehat {OAP} + \widehat {OBS} = 180^\circ \)

và giả sử \(\widehat {OAP} \ge 90^\circ ,\)

Xét ∆PAO ta có: \(\widehat {PAO} > \widehat {APO} \Rightarrow OP > AO\)

mà AO là bán kính, do đó P nằm ngoài (O).

Mặt khác \(EP = ES\) (cmt)

\(⇒ SO = PO > OA\) nên S nằm ngoài (O)

b. Vì OE vuông góc với dây CD nên ta có: \(CE = DE\) (định lí đường kính dây cung)

mà \(EP = ES\) (cmt)

\(⇒ EP – CE = ES – DE\) hay \(PC = DS\).

 HocTot.Nam.Name.Vn