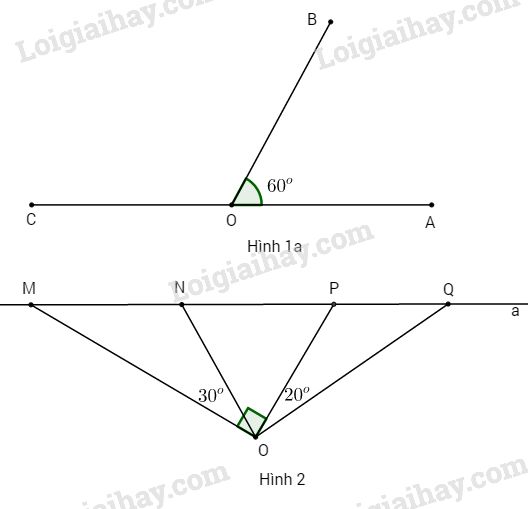
Đề kiểm tra 15 phút - Đề số 7 - Chương 2 - Hình học 6Giải Đề kiểm tra 15 phút - Đề số 7 - Chương 2 - Hình học 6 Đề bài Câu 1. (4 điểm) Cho hai góc kề bù \(\widehat {AOB}\) và \(\widehat {BOC}.\) a) Biết \(\widehat {AOB} = {60^o}.\) Tính \(\widehat {BOC}.\) b) Biết \(\widehat {AOB} - \widehat {BOC} = {36^o}.\) Tính \(\widehat {AOB}\) và \(\widehat {BOC}.\) Câu 2. (6 điểm) Trên đường thẳng a lấy điểm M, N, P, Q theo thứ tự đó. Gọi O là điểm nằm ngoài đường thẳng a. Biết \(\widehat {MON} = {30^o},\)\(\widehat {POQ} = {20^o},\) \(\widehat {MOP} = {90^o}.\) Tính \(\widehat {NOP},\widehat {NOQ},\widehat {MOQ}.\) Phương pháp giải - Xem chi tiết Hai góc bù nhau là hai góc có tổng số đo bằng \(180^\circ \) Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) Ngược lại, nếu \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\). Lời giải chi tiết
HocTot.Nam.Name.Vn
|