Nội dung từ Loigiaihay.Com
Câu hỏi:
Tìm giao điểm đồ thị \(y = 2x - 4\)với trục, tung trục hoành và vẽ đồ thị của hàm số lên mặt phẳng tọa độ \(Oxy\). Tính diện tích của tam giác tạo bởi hai giao điểm và gốc tọa độ.
- A \({S_{OAB}} = 8\)
- B \({S_{OAB}} = 16\)
- C \({S_{OAB}} = 4\)
- D \({S_{OAB}} = 2\)
Phương pháp giải:
Xét đồ thị \(y = x + b\) cắt 2 trục \(Ox\) và \(Oy\) tại 2 điểm \(A,\,\,B\)\( \Rightarrow {S_{OAB}} = \dfrac{{OA.OB}}{2}\)
Lời giải chi tiết:
Cho \(x = 0 \Rightarrow y = - 4\).
Cho \(y = 0 \Rightarrow x = 2\).
Do đó đồ thị \(y = 2x - 4\) cắt trục Ox tại \(A\left( {2;0} \right)\) và cắt trục Oy điểm \(B\left( {0; - 4} \right)\).
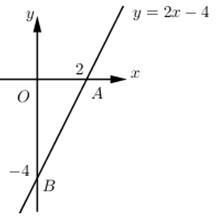
Ta có \(OA = 2\) và \(OB = 4\). Suy ra \({S_{OAB}} = \dfrac{{OA.OB}}{2} = \dfrac{{2.4}}{2} = 4\)













