Phương pháp giải:

Nhận xét. Đề bài cho có thể bị sai ở chỗ " là thể tích khối cầu ngoại tiếp khối lập phương đó là thể tích khối lập phương đó " phải sửa thành chữ " là thể tích khối cầu ngoại tiếp khối lập phương đó và thể tích khối lập phương đó ". Khi đó ta có lời giải như sau.

 Tìm bán kính của mặt cầu ngoại tiếp hình lập phương, sai đó dùng công thức để tính thể tích của mặt cầu ngoại tiếp và của hình lập phương rồi chia tỉ lệ.

Lời giải chi tiết:

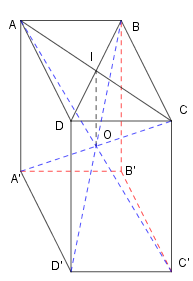
Gọi $\,O=AC'\cap A'C.$ Khi đó do $ABCD.A'B'C'D'$ là hình lập phương nên ta chứng minh được $O$ là tâm của mặt cầu ngoại tiếp hình lập phương này. Bán kính của hình lập phương là $R=OA.$ Áp dụng định lý Py-ta-go cho tam giác vuông $ABC$ ta nhận được $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}}.$

Áp dụng định lý Py-ta-go cho tam giác vuông $ACC'$ ta có $AC'=\sqrt{A{{C}^{2}}+CC{{'}^{2}}}=\sqrt{2{{a}^{2}}+{{a}^{2}}}=a\sqrt{3}.$ Do $O$ là tâm của hình lập phương $ABCD.A'B'C'D'$nên $O$ là trung điểm của $AC'.$ Do đó $AO=\frac{AC'}{2}=\frac{a\sqrt{3}}{2}.$

Do đó thể tích của mặt cầu ngoại tiếp hình lập phương $ABCD.A'B'C'D'$là ${{V}_{1}}=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi {{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}=\frac{\pi {{a}^{3}}\sqrt{3}}{2}.$ Lại có ${{V}_{2}}={{a}^{3}}.$ Do đó $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\frac{\pi {{a}^{3}}\sqrt{3}}{2}}{{{a}^{3}}}=\frac{\pi \sqrt{3}}{2}.$

Chọn đáp án C.