Nội dung từ Loigiaihay.Com
Câu hỏi:
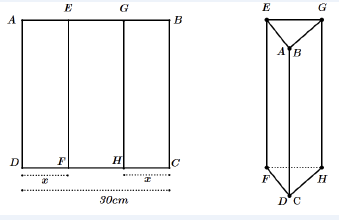
Một tấm kẽm hình vuông ABCD có cạnh bằng 30cm. Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Giá trị của x để thể tích khối lăng trụ lớn nhất là:
- A x=5(cm).
- B x=9(cm).
- C x=8(cm).
- D x=10(cm).
Phương pháp giải:
Tính thể tích khối lăng trụ. Do chiều cao của lăng trụ cố định nên để thể tích lăng trụ là lớn nhất thì diện tích đáy phải lớn nhất. Ta đi tính diện tích đáy, sau đó áp dụng bất đẳng thức Cô-si để tìm giá trị lớn nhất của diện tích đáy.
Lời giải chi tiết:
Thể tích khối lăng trụ là: V=BC.SAEG=30SAEG. Theo giả thiết ta phải có 2x<30⇔x<15.
Ta có tam giác ΔAEG có độ dài các cạnh là AE=AG=x(cm),EG=30−2x(cm) nên diện tích là
S=√15(15−x)(15−x)[15−(30−2x)]=√15(15−x)2(2x−15)(cm2)(1).
Áp dụng bất đẳng thức Cô-si cho (√15−x,√15−x,√2x−15) ta nhận được
√(15−x)2(2x−15)=√(15−x)(15−x)(2x−15)≤√((15−x)+(15−x)+(2x−15)3)3=√53(2).
Thay (2) vào (1) ta nhận được S≤√15.√53=25√3. Do đó V≤30.25√3=750√3(cm3).
Giá trị lớn nhất của thể tích đạt được khi và chỉ khi diện tích SAEG đạt giá trị lớn nhất. Khi đó ta phải có {15−x=2x−150<x<15⇔x=10(cm)
Chọn đáp án D.