Nội dung từ Loigiaihay.Com
Câu hỏi:
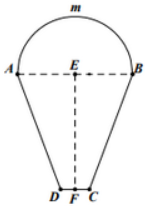
Khí cầu là một túi đựng không khí nóng hay các chất khí trong trường hợp dùng khí heli thì còn được gọi là khinh khí cầu, thường có khối lượng riêng nhỏ hơn không khí xung quanh và nhờ vào lực đẩy Ác-si-mét có thể bay lên cao trong khí quyển. Ngày nay khí cầu vẫn còn được sử dụng để chở khách du lịch hoặc vận chuyển hàng hóa vì chi phí rẻ. Giả sử mặt cắt theo chiều thẳng đứng của một khí cầu có dạng như hình bên phải. Biết cung AmB là nửa đường tròn đường kính 8 m và ABCD là hình thang cân có chiều cao 8m và \(CD = 2m\) Gọi \(V\) là thể tích khí của khối kinh khí cầu đó. Chọn khẳng định đúng trong các khẳng định sau.

- A \(V \in \left( {305;315} \right)\)
- B \(V \in \left( {315;325} \right)\)
- C \(V \in \left( {325;335} \right)\)
- D \(V \in \left( {335;345} \right)\)
Phương pháp giải:
Thể mặt cầu: \(V = \frac{4}{3}\pi {R^3}\)
Tọa độ hóa các điểm trên ABCD tính hình.
Lập hàm số của BC: x(y).
Sử dụng công thức tính thể tích quay xung quanh trục Oy:
\(V = \pi \int\limits_a^b {{x^2}\left( y \right)dy} \)
Lời giải chi tiết:
Thể nửa mặt cầu: \({V_c} = \frac{1}{2}.\frac{4}{3}\pi {.4^3} = \frac{{128\pi }}{3}\)
Điểm \(E\left( {0;0} \right)\), tia EB là Ox.
Khi đó B(4;0), C(1;-8)
\(\overrightarrow {BC} = \left( { - 3; - 8} \right)\). Đường thẳng BC:
\(\begin{array}{l}8\left( {x - 4} \right) - 3y = 0\\ \Leftrightarrow 8x - 3y - 24 = 0\\ \Leftrightarrow x\left( y \right) = \frac{{3y}}{8} + 4\end{array}\)
Thể tích của hình nón cụt tạo bởi EFCB quanh trục Oy là:
\({V_{NC}} = \pi \int\limits_{ - 8}^0 {{x^2}\left( y \right)dy} \)\( = \pi \int\limits_{ - 8}^0 {{{\left( {\frac{{3y}}{8} + 4} \right)}^2}dy} = 56\pi \)
=> \(V = \frac{{128\pi }}{3} + 56\pi \)\( = \frac{{296\pi }}{3} \in \left( {305;315} \right)\)













