Nội dung từ Loigiaihay.Com
Câu hỏi:
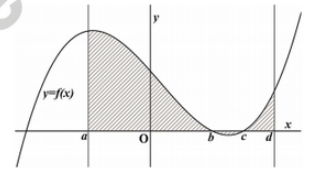
Cho đồ thị hàm số \(y = f(x)\) có đồ thị như hình bên dưới. Tính diện tích \(S\) phần gạch chéo.
- A \(S = \int\limits_b^a {f\left( x \right)dx} - \int\limits_c^d {f\left( x \right)dx} + \int\limits_d^c {f\left( x \right)dx} \)
- B \(S = \int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} + \int\limits_c^d {f\left( x \right)dx} \)
- C \(S = \int\limits_a^b {f\left( x \right)dx} - \int\limits_b^c {f\left( x \right)dx} - \int\limits_c^d {f\left( x \right)dx} \)
- D \(S = \int\limits_a^b {f\left( x \right)dx} - \int\limits_b^c {f\left( x \right)dx} + \int\limits_c^d {f\left( x \right)dx} \)
Phương pháp giải:
Phần diện tích dưới trục Ox mang dấu “-”. Trên trục Ox mang dấu “+”
Lời giải chi tiết:
Từ đồ thị ta thấy,
\(\begin{array}{l}S = \int\limits_a^d {\left| {f\left( x \right)} \right|dx} \\ = \int\limits_a^b {f\left( x \right)dx} - \int\limits_b^c {f\left( x \right)dx} + \int\limits_c^d {f\left( x \right)dx} \end{array}\)













