Phương pháp giải:

Tính đường chéo AC.

Hình chóp đều có đáy là hình vuông và hình chiếu của S đến (ABCD) là tâm của đáy.

Lời giải chi tiết:

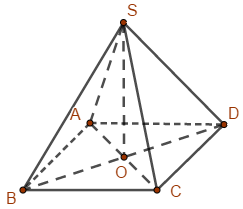
Gọi O là giao điểm của AC và BD.

Khi đó \(d\left( {S,\left( {ABCD} \right)} \right) = SO\)

ABCD là hình vuông nên

\(\begin{array}{l}AC = a\sqrt 2 .\sqrt 2  = 2a =  > AO = a\\ =  > S{O^2} = S{A^2} - A{O^2} = 2{a^2} - {a^2} = {a^2}\\ =  > SO = a\end{array}\)