Nội dung từ Loigiaihay.Com
Câu hỏi:
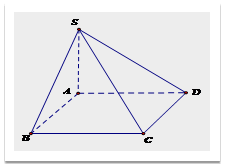
Cho hình chóp \(S.ABCD\)có \(SA \bot \left( {ABCD} \right)\)), đáy\(ABCD\) là hình chữ nhật. Biết\(SA = a,\)\(AD = 2a,\)\(AB = a\sqrt 3 \,.\) Khoảng cách từ điểm \(B\) đến mặt phẳng\(\left( {SCD} \right)\) bằng
- A \(\dfrac{{3a\sqrt 7 }}{7}\).
- B \(\dfrac{{2a\sqrt 5 }}{5}\).
- C \(\dfrac{{3a\sqrt 2 }}{2}\).
- D \(\dfrac{{a\sqrt 3 }}{2}\)
Phương pháp giải:
+ Kẻ \(AH \bot SD\)
+ Chứng minh \(CD \bot \left( {SAD} \right)\), \(AB//\left( {SCD} \right)\)
+ Nếu \(AB//\left( \alpha \right)\) thì \(d\left( {B,\left( \alpha \right)} \right) = d\left( {A,\left( \alpha \right)} \right)\).
+ Trong tam giác \(ABC\) vuông tại A có đường cao AH thì: \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
Lời giải chi tiết:
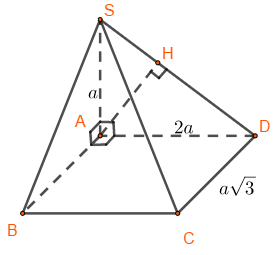
Kẻ \(AH \bot SD\)
\(\left. \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right)\)
\( \Rightarrow CD \bot AH\)
Mà \(AH \bot SD\) nên \(AH \bot \left( {SCD} \right)\)
\( \Rightarrow AH = d\left( {A,\left( {SCD} \right)} \right)\)
\(\begin{array}{l}AB//CD \Rightarrow AB//\left( {SCD} \right)\\ \Rightarrow d\left( {B,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right) = AH\\\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}}\\ \Rightarrow AH = \dfrac{{2a\sqrt 5 }}{5}\end{array}\)













