Phương pháp giải:

- Trong $\left( {SBC} \right)$ kẻ $BH \bot SC\,\,\left( {H \in SC} \right)$, chứng minh $DH \bot SC$ và suy ra $\Rightarrow \angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \angle \left( {BH;DH} \right)$

- Xét 2 trường hợp $\widehat {BHD} = {60^0}$ hoặc $\angle BHD = {120^0}$.

- Chứng minh $\Delta BDH$ cân tại $H$, từ đó tính $HO$ theo $a$ với $O = AC \cap BD$.

- Chứng minh $\Delta SAC \sim \Delta OHC\,\,\left( {g.g} \right)$ $\Rightarrow \dfrac{{SA}}{{OH}} = \dfrac{{SC}}{{OC}}$. Giải phương trình tìm $SA$ theo $a$.

Lời giải chi tiết:

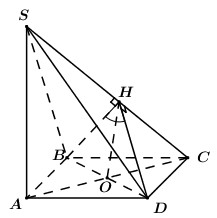
Gọi $O = AC \cap BD$, do $ABCD$ là hình thoi nên $AC \bot BD$ tại $O$.

Ta có: $\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC$.

Trong $\left( {SBC} \right)$ kẻ $BH \bot SC\,\,\left( {H \in SC} \right)$ ta có: $\left\{ \begin{array}{l}SC \bot BH\\SC \bot BD\end{array} \right. \Rightarrow SC \bot \left( {BDH} \right) \Rightarrow SC \bot DH$.

Ta có: $\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {SCD} \right) = SC\\BH \subset \left( {SBC} \right),\,\,BH \bot SC\\DH \subset \left( {SCD} \right),\,\,DH \bot SC\end{array} \right.$ $\Rightarrow \angle \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \angle \left( {BH;DH} \right) = {60^0}$

$\Rightarrow \widehat {BHD} = {60^0}$ hoặc $\angle BHD = {120^0}$.

Xét $\Delta ABD$ có $AB = AD = a$, $\angle BAD = {180^0} - \angle ABC = {60^0}$ (hai góc trong cùng phía bù nhau) $\Rightarrow \Delta ABD$ đều cạnh $a$ $\Rightarrow BD = a,\,\,AO = \dfrac{{a\sqrt 3 }}{2}$ $\Rightarrow BO = \dfrac{1}{2}BD = \dfrac{a}{2}$.

Xét $\Delta SAB$ và $\Delta SAD$ có:

$\begin{array}{l}\angle SAB = \angle SAD = {90^0}\\SA\,\,chung\\AB = AD = a\end{array}$

$\Rightarrow \Delta SAB = \Delta SAD$ (2 cạnh góc vuông) $\Rightarrow SB = SD$.

Xét $\Delta SBC$ và $\Delta SDC$ có:

$\begin{array}{l}SB = SD\,\,\left( {cmt} \right)\\SC\,\,chung\\BC = DC = a\end{array}$

$\Rightarrow \Delta SBC = \Delta SDC\,\,\,\left( {c.c.c} \right)$$\Rightarrow BH = DH$ (2 đường cao tương ứng) $\Rightarrow \Delta BDH$ cân tại $H$ $\Rightarrow HO$ là đường trung tuyến đồng thời là đường cao và đường phân giác $\Rightarrow HO \bot BD$ và $\angle BHO = \dfrac{1}{2}\angle BHD$.

Ta có: $SC \bot \left( {BDH} \right)\,\,\left( {cmt} \right) \Rightarrow SC \bot OH$.

Xét $\Delta SAC$ và $\Delta OHC$ có: $\angle SCA$ chung, $\angle SAC = \angle OHC = {90^0}$, suy ra $\Delta SAC \sim \Delta OHC\,\,\left( {g.g} \right)$.

$\Rightarrow \dfrac{{SA}}{{OH}} = \dfrac{{SC}}{{OC}} \Rightarrow SA = \dfrac{{OH.SC}}{{OC}}\,\,\left( * \right)$, với $OC = OA = \dfrac{{a\sqrt 3 }}{2}$, $SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {S{A^2} + 3{a^2}}$.

TH1: $\angle BHD = {60^0} \Rightarrow \angle BHO = {30^0}$.

Xét tam giác vuông $BHO$ có: $OH = BO.\cot {30^0} = \dfrac{{a\sqrt 3 }}{2} = OC$ (Vô lí do $OH < OC$ - quan hệ đường vuông góc, đường xiên).

TH1: $\angle BHD = {120^0} \Rightarrow \angle BHO = {60^0}$.

Xét tam giác vuông $BHO$ có: $OH = BO.\cot {60^0} = \dfrac{a}{2}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{6}$.

Thay vào (*) ta có:

$\begin{array}{l}SA = \dfrac{{\dfrac{{a\sqrt 3 }}{6}.\sqrt {S{A^2} + 3{a^2}} }}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow SA = \dfrac{{\sqrt {S{A^2} + 3{a^2}} }}{3}\\ \Leftrightarrow 9S{A^2} = S{A^2} + 3{a^2} \Leftrightarrow 8S{A^2} = 3{a^2}\\ \Leftrightarrow S{A^2} = \dfrac{{3{a^2}}}{8} \Leftrightarrow SA = \dfrac{{a\sqrt 6 }}{4}\end{array}$

Chọn A.