Nội dung từ Loigiaihay.Com
Câu hỏi:
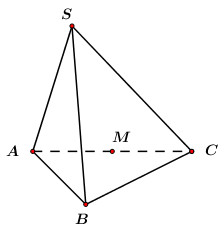
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy là \(a\sqrt 3 ,\) cạnh bên bằng \(2a.\) Điểm \(M\) là trung điểm cạnh \(AC.\) Khoảng cách giữa \(BM\) và \(SC\) bằng:
- A \(\dfrac{{a\sqrt {15} }}{5}\)
- B \(a\sqrt {\dfrac{{11}}{{47}}} \)
- C \(\dfrac{{a\sqrt {39} }}{{13}}\)
- D \(\dfrac{{a\sqrt 3 }}{{13}}\)
Phương pháp giải:
Gọi \(G\) là trọng tâm \(\Delta ABC\) \( \Rightarrow SG \bot \left( {ABC} \right).\)
Qua \(C\) dựng đường thẳng \(d\) song song với \(BM\) cắt \(AB\) tại \(D.\)
\( \Rightarrow BM//\left( {SCD} \right)\) \( \Rightarrow d\left( {BM;\,\,SC} \right) = d\left( {BM;\,\,\left( {SCD} \right)} \right) = d\left( {G;\,\,\left( {SCD} \right)} \right)\)
Lời giải chi tiết:
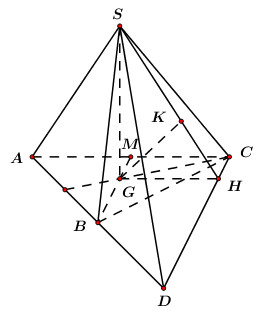
Gọi \(G\) là trọng tâm \(\Delta ABC\) \( \Rightarrow SG \bot \left( {ABC} \right).\)
Qua \(C\) dựng đường thẳng \(d\) song song với \(BM\) cắt \(AB\) tại \(D.\)
\( \Rightarrow BM//\left( {SCD} \right)\) \( \Rightarrow d\left( {BM;\,\,SC} \right) = d\left( {BM;\,\,\left( {SCD} \right)} \right) = d\left( {G;\,\,\left( {SCD} \right)} \right)\)
Ta có: \(CD//BM \Rightarrow CD \bot AC.\)
Từ \(G\) kẻ \(GH \bot CD = \left\{ H \right\}\)
\( \Rightarrow MCHG\) là hình chữ nhật. (dhnb)
\( \Rightarrow GH = MC = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 3 }}{2}\)
Trong mặt phẳng \(\left( {SGH} \right),\) kẻ \(GK \bot SH.\)
Ta có: \(\left\{ \begin{array}{l}CD \bot GH\\CD \bot SG\end{array} \right. \Rightarrow CD \bot \left( {SGH} \right)\) \( \Rightarrow CD \bot GK\)
\(\begin{array}{l} \Rightarrow GK \bot \left( {SCD} \right)\\ \Rightarrow d\left( {BM,\,\,SC} \right) = d\left( {G;\,\,\left( {SCD} \right)} \right) = GK\end{array}\)
Ta có: \(\Delta ABC\) là tam giác đều cạnh \(a\sqrt 3 \) \( \Rightarrow BM = \dfrac{{a\sqrt 3 .\sqrt 3 }}{2} = \dfrac{{3a}}{2}\)
\( \Rightarrow BG = \dfrac{2}{3}BM = \dfrac{2}{3}.\dfrac{3}{2}a = a.\)
Áp dụng định lý Pitago cho \(\Delta SBG\) vuông tại \(G\) ta có:
\(SG = \sqrt {S{B^2} - B{G^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = a\sqrt 3 .\)
Áp dụng hệ thức lượng cho \(\Delta SGH\) vuông tại \(G\) có đường cao \(GK\) ta có:
\(GK = \dfrac{{SG.GH}}{{\sqrt {S{G^2} + G{H^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}} }} = \dfrac{{a\sqrt {15} }}{5}.\)
Chọn A.













