Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho tứ diện \(ABCD\) có \(AB,\,\,AC,\,\,AD\) đôi một vuông góc với nhau và \(AD = 2\), \(AB = AC = 1\). Gọi \(I\) là trung điểm của đoạn thẳng \(BC\), khoảng cách giữa \(AI\) và \(BD\) bằng:
- A \(\dfrac{3}{2}\)
- B \(\dfrac{2}{{\sqrt 5 }}\)
- C \(\dfrac{{\sqrt 5 }}{2}\)
- D \(\dfrac{{2}}{{3}}\)
Phương pháp giải:
- Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AC,\,\,CD\). Chứng minh \(d\left( {AI;BD} \right) = 2d\left( {M;\left( {ANI} \right)} \right)\).
- Trong \(\left( {MNH} \right)\) kẻ \(MK \bot NH\,\,\left( {K \in NH} \right)\), chứng minh \(MK \bot \left( {ANI} \right)\).
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
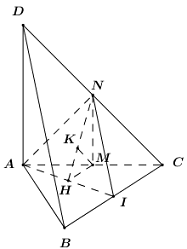
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AC,\,\,CD\).
Ta có \(\left\{ \begin{array}{l}AD \bot AC\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {ABC} \right)\), lại có \(AD\parallel MN\) (do \(MN\) là đường trung bình của tam giác \(ACD\)) \( \Rightarrow MN \bot \left( {ABC} \right)\).
Ta có: \(IN\parallel BD\) (\(IN\) là đường trug bình của tam giác \(BCD\)) \( \Rightarrow BD\parallel \left( {ANI} \right) \supset AI\).
\( \Rightarrow d\left( {AI;BD} \right) = d\left( {BD;\left( {ANI} \right)} \right) = d\left( {B;\left( {ANI} \right)} \right)\).
Lại có:
\(\begin{array}{l}BC \cap \left( {ANI} \right) = I \Rightarrow \dfrac{{d\left( {B;\left( {ANI} \right)} \right)}}{{d\left( {C;\left( {ANI} \right)} \right)}} = \dfrac{{BI}}{{CI}} = 1\\ \Rightarrow d\left( {B;\left( {ANI} \right)} \right) = d\left( {C;\left( {ANI} \right)} \right)\\CM \cap \left( {ANI} \right) = A \Rightarrow \dfrac{{d\left( {C;\left( {ANI} \right)} \right)}}{{d\left( {M;\left( {ANI} \right)} \right)}} = \dfrac{{CA}}{{MA}} = 2\\ \Rightarrow d\left( {C;\left( {ANI} \right)} \right) = 2d\left( {M;\left( {ANI} \right)} \right)\\ \Rightarrow d\left( {B;\left( {ANI} \right)} \right) = 2d\left( {M;\left( {ANI} \right)} \right)\end{array}\)
Gọi \(H\) là trung điểm của \(AI \Rightarrow MH\parallel IC\) (\(MH\) là đườn trung bình của tam giác \(AIC\)).
Mà \(\Delta ABC\) có \(AB = AC = 1\) nên là tam giác vuông cân tại \(A\) \( \Rightarrow AI \bot BC\) hay \(AI \bot IC\).
\( \Rightarrow MH \bot AI\).
Ta có: \(\left\{ \begin{array}{l}AI \bot MH\\AI \bot MN\,\,\left( {MN \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AI \bot \left( {MNH} \right)\).
Trong \(\left( {MNH} \right)\) kẻ \(MK \bot NH\,\,\left( {K \in NH} \right)\) ta có: \(\left\{ \begin{array}{l}MK \bot NH\\MK \bot AI\,\,\left( {AI \bot \left( {MNH} \right)} \right)\end{array} \right. \Rightarrow MK \bot \left( {ANI} \right)\).
\( \Rightarrow d\left( {M;\left( {ANI} \right)} \right) = MK \Rightarrow d\left( {AI;BD} \right) = 2MK\).
Ta có \(MN = \dfrac{1}{2}AD = 1,\,\,MH = \dfrac{1}{2}CI = \dfrac{1}{4}BC = \dfrac{1}{4}AB\sqrt 2 = \dfrac{{\sqrt 2 }}{4}\).
Áp dụng hệ thức lượng trong tam giác vuông \(MNH\) có: \(MK = \dfrac{{MN.MH}}{{\sqrt {M{N^2} + M{H^2}} }} = \dfrac{{1.\dfrac{{\sqrt 2 }}{4}}}{{\sqrt {1 + \dfrac{1}{8}} }} = \dfrac{1}{3}\).
Vậy \(d\left( {AI;BD} \right) = \dfrac{2}{3}\).
Chọn D.













