Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho tứ diện \(ABCD\) có \(\angle ABC = \angle ADC = \angle BCD = {90^0}\), \(BC = 2a\), \(CD = a\), góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\) bằng \({60^0}\). Tính khoảng cách giữa hai đường thẳng \(AC\) và \(BD\).
- A \(\dfrac{{a\sqrt 6 }}{{\sqrt {31} }}\)
- B \(\dfrac{{2a\sqrt 6 }}{{\sqrt {31} }}\)
- C \(\dfrac{{2a\sqrt 3 }}{{\sqrt {31} }}\)
- D \(\dfrac{{a\sqrt 3 }}{{\sqrt {31} }}\)
Phương pháp giải:
- Gọi \(E\) là hình chiếu của \(A\) lên \(\left( {ABC} \right)\), chứng minh \(BCDE\) là hình chữ nhật.
- Gọi \(O = BD \cap CE\) là \(A'\) là trung điểm của \(AE\), chứng minh \(d\left( {AC;BD} \right) = d\left( {E;\left( {A'BD} \right)} \right)\).
- Trong \(\left( {BCDE} \right)\) kẻ \(EH \bot BD\,\,\left( {H \in BD} \right)\), trong \(\left( {OA'E} \right)\) kẻ \(EK \bot A'H\,\,\left( {K \in A'H} \right)\), chứng minh \(EK \bot \left( {A'BD} \right)\).
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
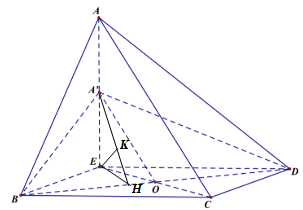
Gọi \(E\) là hình chiếu của \(A\) lên \(\left( {ABC} \right)\) \( \Rightarrow AE \bot \left( {BCD} \right)\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AE\\BC \bot AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BC \bot \left( {ABE} \right) \Rightarrow BC \bot BE\).
\(\left\{ \begin{array}{l}CD \bot AE\\CD \bot AD\,\,\left( {gt} \right)\end{array} \right. \Rightarrow CD \bot \left( {AED} \right) \Rightarrow CD \bot DE\).
Do đó \(BCDE\) là hình chữ nhật (Tứ giác có 3 góc vuông).
Ta có \(AE \bot \left( {BCDE} \right) \Rightarrow EB\) là hình chiếu của \(AB\) lên \(\left( {BCDE} \right)\)
\( \Rightarrow \angle \left( {AB;\left( {BCD} \right)} \right) = \angle \left( {AB;EB} \right) = \angle ABE = {60^0}\).
Gọi \(O = BD \cap CE\) là \(A'\) là trung điểm của \(AE\), suy ra \(OA'\parallel AC\) (tính chất đường trung bình).
\( \Rightarrow AC\parallel \left( {A'BD} \right) \supset BD \Rightarrow d\left( {AC;BD} \right) = d\left( {AC;\left( {A'BD} \right)} \right) = d\left( {A;\left( {A'BD} \right)} \right)\).
Lại có \(AE \cap \left( {A'BD} \right) = A' \Rightarrow \dfrac{{d\left( {A;\left( {A'BD} \right)} \right)}}{{d\left( {E;\left( {A'BD} \right)} \right)}} = \dfrac{{AA'}}{{EA'}} = 1\).
\( \Rightarrow d\left( {A;\left( {A'BD} \right)} \right) = d\left( {E;\left( {A'BD} \right)} \right)\).
Trong \(\left( {BCDE} \right)\) kẻ \(EH \bot BD\,\,\left( {H \in BD} \right)\), trong \(\left( {OA'E} \right)\) kẻ \(EK \bot A'H\,\,\left( {K \in A'H} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot EH\\BD \bot A'E\end{array} \right. \Rightarrow BD \bot \left( {A'HE} \right) \Rightarrow BD \bot EK\\\left\{ \begin{array}{l}EK \bot A'H\\EK \bot BD\end{array} \right. \Rightarrow EK \bot \left( {A'BD} \right) \Rightarrow d\left( {E;\left( {A'BD} \right)} \right) = EK\end{array}\)
Xét tam giác vuông \(ABE\) có: \(AE = BE.\tan {60^0} = a\sqrt 3 \Rightarrow A'E = \dfrac{{a\sqrt 3 }}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(EH = \dfrac{{EB.ED}}{{\sqrt {E{B^2} + E{D^2}} }} = \dfrac{{a.2a}}{{\sqrt {{a^2} + 4{a^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}\)
\(EK = \dfrac{{EA'.EH}}{{\sqrt {EA{'^2} + E{H^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{{2a}}{{\sqrt 5 }}}}{{\sqrt {\dfrac{{3{a^2}}}{4} + \dfrac{{4{a^2}}}{5}} }} = \dfrac{{2a\sqrt {93} }}{{31}} = \dfrac{{2a\sqrt 3 }}{{\sqrt {31} }}\).
Chọn C.













