Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA = SB = SC = SD = \(a\sqrt 2 \). Gọi A’, C’ lần lượt là trung điểm SA, SC. Tính \({d_{\left[ {S'\left( {A'BC'} \right)} \right]}}\).
- A \(\dfrac{{a\sqrt {42} }}{{28}}\).
- B \(\dfrac{{a\sqrt {42} }}{{14}}\).
- C \(\dfrac{{a\sqrt {6} }}{{14}}\).
- D \(\dfrac{{a\sqrt {7} }}{{14}}\).
Phương pháp giải:
- Đổi \(d\left( {S;\left( {A'BC'} \right)} \right)\) sang \(d\left( {O;\left( {A'BC'} \right)} \right)\) với \(O = AC \cap BD\).
- Gọi \(M = A'C' \cap SO\), chứng minh \(A'C' \bot \left( {BOM} \right)\).
- Trong \(\left( {BOM} \right)\) kẻ \(OH \bot BM\,\,\left( {H \in BM} \right)\), chứng minh \(OH \bot \left( {A'BC'} \right)\).
- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính \(OH\).
Lời giải chi tiết:
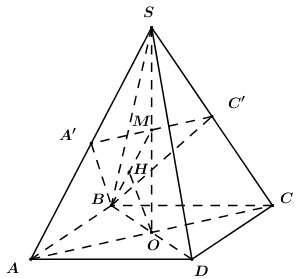
+ Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).
Trong \(\left( {SAC} \right)\) gọi \(M = A'C' \cap SO\).
+ \(A'C'\) là đường trung bình của tam giác \(SAC \Rightarrow A'C'\parallel AC\).
+ Áp dụng định lí Ta-lét: \(\dfrac{{SA'}}{{SA}} = \dfrac{{SM}}{{SO}} = \dfrac{1}{2} \Rightarrow M\) là trung điểm của \(SO\).
+ \(SO \cap \left( {A'BC'} \right) = M \Rightarrow \dfrac{{d\left( {S;\left( {A'BC'} \right)} \right)}}{{d\left( {O;\left( {A'BC'} \right)} \right)}} = \dfrac{{SM}}{{OM}} = 1\) \( \Rightarrow d\left( {S;\left( {A'BC'} \right)} \right) = d\left( {O;\left( {A'BC'} \right)} \right)\).
+ \(\Delta SAB = \Delta SCB\,\,\left( {c.c.c} \right) \Rightarrow BA' = BC'\) \( \Rightarrow \Delta BA'C'\) cân tại \(B\) \( \Rightarrow BM \bot A'C'\).
Trong \(\left( {BOM} \right)\) kẻ \(OH \bot BM\,\,\left( {H \in BM} \right)\).
+ \(\left\{ \begin{array}{l}A'C' \bot MO\\A'C' \bot BM\end{array} \right. \Rightarrow A'C' \bot \left( {BOM} \right) \Rightarrow A'C' \bot OH\).
+ \(\left\{ \begin{array}{l}OH \bot A'C'\\OH \bot BM\end{array} \right. \Rightarrow OH \bot \left( {A'BC'} \right)\) \( \Rightarrow d\left( {O;\left( {A'BC'} \right)} \right) = OH\).
+ \(ABCD\) là hình vuông cạnh \(a\) \( \Rightarrow BD = a\sqrt 2 \Rightarrow BO = \dfrac{{a\sqrt 2 }}{2}\).
+ \(\Delta SBO:\,\,SO = \sqrt {S{B^2} - B{O^2}} = \sqrt {2{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 6 }}{2}\) \( \Rightarrow OM = \dfrac{{a\sqrt 6 }}{4}\).
+ \(\Delta BOM:\,\,\,\,OH = \dfrac{{BO.OM}}{{\sqrt {B{O^2} + O{M^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.\dfrac{{a\sqrt 6 }}{4}}}{{\sqrt {\dfrac{{{a^2}}}{2} + \dfrac{{3{a^2}}}{8}} }} = \dfrac{{a\sqrt {42} }}{{14}}\).
Vậy \(d\left( {S;\left( {A'BC'} \right)} \right) = \dfrac{{a\sqrt {42} }}{{14}}\).













