Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA = a, \(SA \bot \left( {ABCD} \right)\). Gọi M, N lần lượt là trung điểm của AD, DC. Góc giữa (SBM) và (ABCD) bằng \({45^0}\). Tính \({d_{\left[ {D;\left( {SBM} \right)} \right]}}\).
- A \(\dfrac{{a\sqrt 3 }}{3}\)
- B \(\dfrac{{a\sqrt 3 }}{2}\)
- C \(\dfrac{{a\sqrt 2 }}{2}\)
- D \(\dfrac{{a\sqrt 2 }}{3}\)
Phương pháp giải:
+ Trong \(\left( {ABCD} \right)\) gọi \(I = AN \cap BM\). Chứng minh \(AN \bot BM\) tại \(I\).
+ Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
+ Trong \(\left( {SAI} \right)\) kẻ \(AH \bot SI\,\,\left( {H \in SI} \right)\), chứng minh \(AH \bot \left( {SBM} \right)\).
+ Đổi tính \(d\left( {D;\left( {SBM} \right)} \right)\) sang tính \(d\left( {A;\left( {SBM} \right)} \right)\).
Lời giải chi tiết:
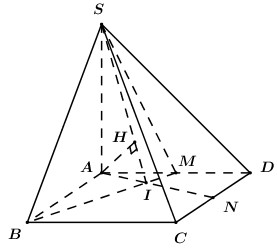
Trong \(\left( {ABCD} \right)\) gọi \(I = AN \cap BM\).
+ Xét \(\Delta ADN\) và \(\Delta ABM\) có: \(AD = AB,\,\,DN = BM\).
\( \Rightarrow \Delta ADN = \Delta ABM\) (2 cạnh góc vuông) \( \Rightarrow \angle NAD = \angle MBA\).
Mà \(\angle NAD + \angle NAB = \angle BAD = {90^0}\) \( \Rightarrow \angle MBA + \angle NAB = {90^0}\) \( \Rightarrow \Delta ABI\) vuông tại \(I\) hay \(AI \bot BM\).
+ \(\left\{ \begin{array}{l}BM \bot AI\\BM \bot SA\end{array} \right. \Rightarrow BM \bot \left( {SAI} \right) \Rightarrow BM \bot SI\).
+ \(\left\{ \begin{array}{l}\left( {SBM} \right) \cap \left( {ABCD} \right) = BM\\SI \subset \left( {SBM} \right),\,\,SI \bot BM\\AI \subset \left( {ABCD} \right),\,\,AI \bot BM\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBM} \right);\left( {ABCD} \right)} \right) = \angle \left( {SI;AI} \right) = \angle SIA = {45^0}\).
Trong (SAI) kẻ \(AH \bot SI\,\,\left( {H \in SI} \right)\)
+ \(\left\{ \begin{array}{l}AH \bot SI\\AH \bot BM\end{array} \right. \Rightarrow AH \bot \left( {SBM} \right)\) \( \Rightarrow d\left( {A;\left( {SBM} \right)} \right) = AH\).
+ \(DA \cap \left( {SBM} \right) = M \Rightarrow \dfrac{{d\left( {D;\left( {SBM} \right)} \right)}}{{d\left( {A;\left( {SBM} \right)} \right)}} = \dfrac{{DM}}{{AM}} = 1\) \( \Rightarrow d\left( {D;\left( {SBM} \right)} \right) = d\left( {A;\left( {SBM} \right)} \right) = AH\).
+ \(\Delta SAI\) có \(\angle SIA = {45^0}\) nên là tam giác vuông cân tại A \( \Rightarrow AH = \dfrac{{SA\sqrt 2 }}{2} = \dfrac{{a\sqrt 2 }}{2}\).
Vậy \(d\left( {D;\left( {SBM} \right)} \right) = \dfrac{{a\sqrt 2 }}{2}\).













