Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 6cm\) và \(AC = 8cm\) . Các phân giác trong và ngoài của góc \(B\) cắt đường thẳng\(AC\) lần lượt tại \(M\) và \(N\). Tính các đoạn thẳng \(AM\)và \(AN\).
- A \(AM = 3cm\,\,;\,\,\,AN = 9cm\)
- B \(AM = 2cm\,\,;\,\,\,AN = 18cm\)
- C \(AM = 4cm\,\,;\,\,\,AN = 9cm\)
- D \(AM = 3cm\,\,;\,\,\,AN = 12cm\)
Phương pháp giải:
Sử dụng định lý Pitago cho tam giác ABC vuông tại A để tính độ dài cạnh BC.
Theo đề bài ta có AM, AN lần lượt là các đường phân giác trong và ngoài của góc B.
Khi đó áp dụng tính chất tia phân giác của một góc ta có: \(\frac{{AM}}{{MC}} = \frac{{AN}}{{NC}} = \frac{{AB}}{{BC}}.\)
Lời giải chi tiết:
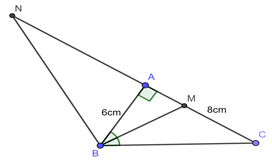
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = 10\left( {cm} \right)\)
Vì \(BM\) là tia phân giác trong của góc \(B \Rightarrow \frac{{MA}}{{MC}} = \frac{{AB}}{{BC}}\) (Tính chất đường phân giác)
\( \Rightarrow \frac{{MA}}{{MC + MA}} = \frac{{AB}}{{BC + AB}} \Rightarrow \frac{{MA}}{{AC}} = \frac{{AB}}{{BC + AB}}\)\( \Rightarrow \frac{{MA}}{8} = \frac{6}{{10 + 6}} \Rightarrow MA = 3cm\)
Vì \(BM;BN\) là tia phân giác trong và ngoài của góc \(B \Rightarrow \angle NBM = {90^0}\)
Áp dụng hệ thức lượng trong \(\Delta ABM\) vuông tại \(B\) có đường cao \(BA\) ta có:
\( \Rightarrow A{B^2} = AM.AN\)\( \Leftrightarrow {6^2} = 3.AN \Leftrightarrow AN = 12\left( {cm} \right)\)
Chọn D.













