Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho chóp tứ giác đều S.ABCD có AB = a và \(SB = \dfrac{{a\sqrt 3 }}{2}\). Tính khoảng cách từ A đến mặt phẳng (SBC).
- A \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 2 }}{4}\)
- B \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{a}{2}\)
- C \(d\left( {A;\left( {SBC} \right)} \right) = a\)
- D \(d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{a\sqrt 2 }}{2}\)
Phương pháp giải:
- Đổi điểm về tính khoảng cách từ O đến (SBC).
- Xác định mặt phẳng chứa O và vuông góc với (SBC).
- Trong mặt phẳng đó kẻ đường thẳng vuông góc với giao tuyến của mặt phẳng đó và (SBC).
- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông.
Lời giải chi tiết:
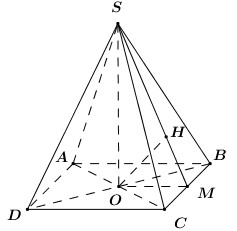
Gọi \(O = AC \cap BD\). Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\).
Ta có: \(AO \cap \left( {SBC} \right) = C \Rightarrow \dfrac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {O;\left( {SBC} \right)} \right)}} = \dfrac{{AC}}{{OC}} = 2\).
\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 2d\left( {O;\left( {SBC} \right)} \right)\).
Gọi M là trung điểm của BC, suy ra OM là đường trung bình của tam giác ABC.
\( \Rightarrow OM\parallel AB\) và \(OM = \dfrac{1}{2}BC = \dfrac{1}{2}AB = \dfrac{a}{2}\). Mà \(AB \bot BC\) nên \(OM \bot BC\).
Ta có: \(\left\{ \begin{array}{l}BC \bot OM\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right)\).
\(\left\{ \begin{array}{l}BC \bot \left( {SOM} \right)\\BC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow \left( {SOM} \right) \bot \left( {SBC} \right)\) và \(\left( {SOM} \right) \cap \left( {SBC} \right) = SM\).
Trong (SOM) kẻ \(OH \bot SM\) ta có:
\(\left\{ \begin{array}{l}\left( {SBC} \right) \bot \left( {SOM} \right)\\\left( {SBC} \right) \cap \left( {SOM} \right) = SM\\OH \subset \left( {SOM} \right),\,\,OH \bot SM\end{array} \right. \Rightarrow OH \bot \left( {SBC} \right)\).
Do đó \(d\left( {O;\left( {SBC} \right)} \right) = OH\) và \(d\left( {A;\left( {SBC} \right)} \right) = 2OH\).
Vì ABCD là hình vuông cạnh a nên \(AC = BD = a\sqrt 2 \) \( \Rightarrow OB = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông SOB có: \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{2{a^2}}}{4}} = \dfrac{a}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông SOM có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}} = \dfrac{4}{{{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{8}{{{a^2}}}\) \( \Rightarrow OH = \dfrac{{a\sqrt 2 }}{4}\).
Vậy \(d\left( {A;\left( {SBC} \right)} \right) = 2OH = \dfrac{{a\sqrt 2 }}{2}\).
Chọn D.













