Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(a\), \(SA\)vuông gócvới mặt phẳng đáy, góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt đáy là \({60^0}\) (minh họa như hình bên). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\). Khoảng cách giữa hai đường thẳng \(SB\) và \(MN\) bằng:
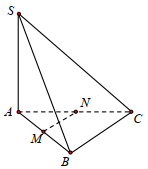
- A \(\dfrac{{3a}}{8}\)
- B \(\dfrac{{3a}}{4}\)
- C \(a\sqrt 6 \)
- D \(\dfrac{{a\sqrt 6 }}{2}\)
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa đường này và mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
- Sử dụng phương pháp đổi đỉnh, đổi về khoảng cách từ \(A\) đến \(\left( {SBC} \right)\).
- Xác định khoảng cách và sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
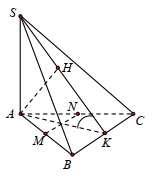
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN\parallel BC \Rightarrow MN\parallel \left( {SBC} \right)\).
\( \Rightarrow d\left( {MN;SB} \right) = d\left( {MN;\left( {SBC} \right)} \right) = d\left( {M;\left( {SBC} \right)} \right)\).
Ta có:
\(\begin{array}{l}AM \cap \left( {SBC} \right) = B \Rightarrow \dfrac{{d\left( {M;\left( {SBC} \right)} \right)}}{{d\left( {A;\left( {SBC} \right)} \right)}} = \dfrac{{MB}}{{AB}} = \dfrac{1}{2}\\ \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right)\end{array}\)
Gọi \(K\) là trung điểm của \(BC\). Vì \(\Delta ABC\) đều nên \(BC \bot AK\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AK\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right.\)\( \Rightarrow BC \bot \left( {SAK} \right)\).
Trong \(\left( {SAK} \right)\) kẻ \(AH \bot SK\,\,\left( {H \in SK} \right)\), ta có: \(\left\{ \begin{array}{l}AH \bot SK\\AH \bot BC\end{array} \right.\)\( \Rightarrow AH \bot \left( {SBC} \right)\).
\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH\).
Tam giác \(ABC\) đều cạnh \(a\) nên \(AK = \dfrac{{a\sqrt 3 }}{2}\).
Ta có: \(BC \bot \left( {SAK} \right) \Rightarrow BC \bot SK\).
Khi đó ta có \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SK \bot BC\\\left( {ABC} \right) \supset AK \bot BC\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SK;AK} \right) = \angle SKA = {60^0}\).
Xét tam giác vuông \(SAK\) có: \(SA = AK.tan{60^0} = \dfrac{{a\sqrt 3 }}{2}.\sqrt 3 = \dfrac{{3a}}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SAK\) ta có:
\(AH = \dfrac{{SA.AK}}{{\sqrt {S{A^2} + A{K^2}} }} = \dfrac{{\dfrac{{3a}}{2}.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {\dfrac{{9{a^2}}}{4} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{3a}}{4}\).
Vậy \(d\left( {MN;SB} \right) = \dfrac{1}{2}AH = \dfrac{{3a}}{8}\).
Chọn A.













